《2025年全程助学与学习评估九年级数学上册浙教版》

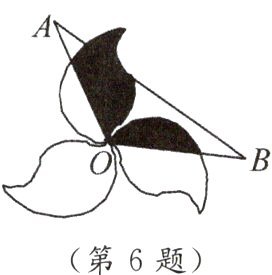
6. 如图,图案由三个叶片组成,绕点 $ O $ 旋转 $ 120^{\circ} $ 后可以和自身重合.若每个叶片的面积为 $ 4cm^2 $,$ \angle AOB $ 为 $ 120^{\circ} $,则图中阴影部分面积和为4$ cm^2 $.
]

答案： 4

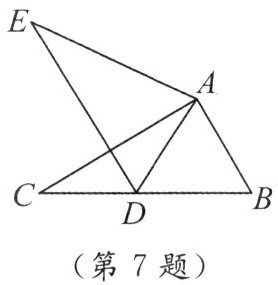
7. 如图,在 $ \triangle ABC $ 中,$ AB = 2 $,$ BC = 3.6 $,$ \angle B = 60^{\circ} $,将 $ \triangle ABC $ 绕点 $ A $ 按顺时针旋转一定角度得到 $ \triangle ADE $,当点 $ B $ 的对应点 $ D $ 恰好落在 $ BC $ 边上时,则 $ CD $ 的长为 1.6.
]

答案： 1.6

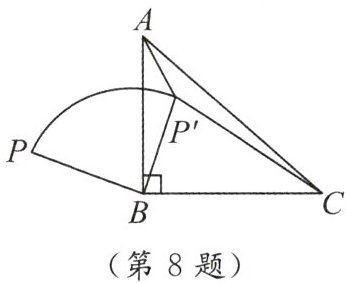
8. 如图,$ P $ 是等腰直角 $ \triangle ABC $ 外一点,把 $ BP $ 绕点 $ B $ 顺时针旋转 $ 90^{\circ} $ 到 $ BP' $,已知 $ \angle AP'B = 135^{\circ} $,$ P'A : P'C = 1 : 3 $,则 $ P'A : PB = $(B)

A.$ 1 : \sqrt{2} $
B.$ 1 : 2 $
C.$ \sqrt{3} : 2 $
D.$ 1 : \sqrt{3} $

答案： B

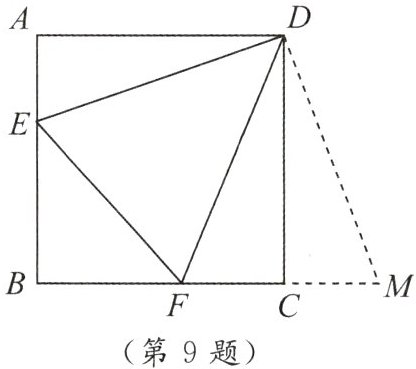
9. 正方形 $ ABCD $ 的边长为 $ 3 $,$ E $,$ F $ 分别是 $ AB $,$ BC $ 边上的点,且 $ \angle EDF = 45^{\circ} $.将 $ \triangle DAE $ 绕点 $ D $ 逆时针旋转 $ 90^{\circ} $,得到 $ \triangle DCM $.
(1)求证：$ EF = FM $.
(2)当 $ AE = 1 $ 时,求 $ EF $ 的长.
]

答案：
(1)见证明过程；
(2)$\frac{5}{2}$。