《2025年全程助学与学习评估九年级数学上册浙教版》

1. 已知线段 $ a $,$ b $,$ c $,其中 $ c $ 是 $ a $ 和 $ b $ 的比例中项,$ a = 4 $,$ b = 9 $,则 $ c = $(B)
A.4
B.6
C.9
D.36

答案： B

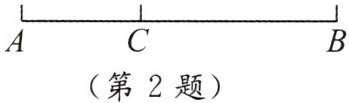
2. 如图,点 $ C $ 是线段 $ AB $ 的黄金分割点,且 $ AC ＜ BC $,$ AC = mBC $,则 $ m $ 的值是(D)

A.$\frac{\sqrt{5} - 1}{2}$
B.$\frac{\sqrt{5} + 1}{2}$
C.$\frac{3 - \sqrt{5}}{2}$
D.$\sqrt{5} - 2$

答案： D

3. 小慈同学在学习了今天的新课后,发现学习内容是一个逐步特殊化的过程,请在横线上填写适当的数值,感受这种特殊化的学习过程.

2

答案： 2

4. 为了美观起见,通常把一本书的宽与长之比设计成黄金比. 已知这本书的宽为 $ 15cm $,则它的长为$\frac{15(\sqrt{5}+1)}{2}$$cm$.

答案： $\frac{15(\sqrt{5}+1)}{2}$

5. 若线段 $ y $ 是线段 $ x $,$ z $ 的比例中项,且 $ x : z = 3 : 4 $,求 $ y : z $ 的值.

答案： 因为线段$y$是线段$x$，$z$的比例中项，所以$x:y = y:z$，即$y^2=xz$。
已知$x:z = 3:4$，设$x = 3k$，$z = 4k$（$k＞0$）。
将$x = 3k$，$z = 4k$代入$y^2=xz$，得$y^2=3k×4k = 12k^2$，则$y = 2\sqrt{3}k$（线段长度为正数，舍去负值）。
所以$y:z=2\sqrt{3}k:4k = \sqrt{3}:2$。
$\sqrt{3}:2$

6. 若线段 $ AB = 6cm $,点 $ C $ 是线段 $ AB $ 的一个黄金分割点,则 $ AC $ 的长为多少？

答案： 分两种情况：
1. 当AC为较长线段时，由黄金分割定义得$AC=\frac{\sqrt{5}-1}{2}AB$，代入$AB=6\mathrm{cm}$，得$AC=6×\frac{\sqrt{5}-1}{2}=3(\sqrt{5}-1)=3\sqrt{5}-3\mathrm{cm}$；
2. 当AC为较短线段时，$BC=\frac{\sqrt{5}-1}{2}AB=3\sqrt{5}-3\mathrm{cm}$，则$AC=AB-BC=6-(3\sqrt{5}-3)=9-3\sqrt{5}\mathrm{cm}$。
综上，$AC$的长为$(3\sqrt{5}-3)\mathrm{cm}$或$(9-3\sqrt{5})\mathrm{cm}$。