1. $\odot O的半径为5\mathrm{cm}$,$A为OP$的中点,若$OP = 6\mathrm{cm}$,则点$A与\odot O$的位置关系是(
A.点$A在\odot O$上
B.点$A在\odot O$内
C.点$A在\odot O$外
D.不能确定
B
)A.点$A在\odot O$上
B.点$A在\odot O$内
C.点$A在\odot O$外
D.不能确定
答案:
B
2. 以下命题:(1)同圆中等弧对等弦;(2)圆心角相等,它们所对的弧长也相等;(3)三点确定一个圆;(4)平分弦的直径必垂直于这条弦. 其中正确的命题的个数是(
A.1个
B.2个
C.3个
D.4个
A
)A.1个
B.2个
C.3个
D.4个
答案:
A
3. 如图,在半径为$5的\odot O$中,若弦$AB的长为8$,则弦心距$OC = $(
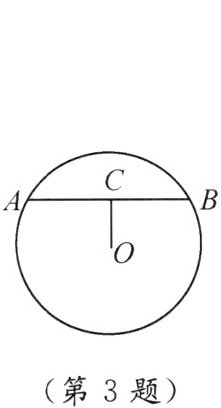
A.2
B.3
C.4
D.6
]
B
)
A.2
B.3
C.4
D.6
]
答案:
B
4. 如图,在平面直角坐标系中,$\odot A经过原点O$,并且分别与$x$轴,$y轴交于B$,$C$两点,已知$B(8,0)$,$C(0,6)$,则$\odot A$的半径为(
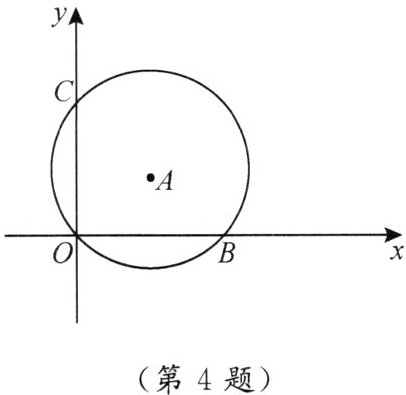
A.3
B.4
C.5
D.8
C
)
A.3
B.4
C.5
D.8
答案:
C
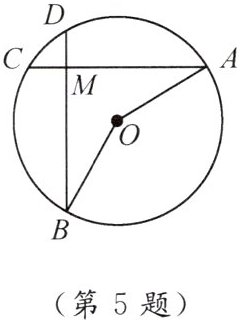
5. 如图,在$\odot O$中,弦$AC$,$BD相交于点M$,且$\angle A= \angle B$.
(1)求证:$AC = BD$.
(2)若$OA = 2$,$\angle A = 30^{\circ}$,当$AC\perp BD$时,求$\overset{\frown}{CD}$的长.
]
(1)求证:$AC = BD$.
(2)若$OA = 2$,$\angle A = 30^{\circ}$,当$AC\perp BD$时,求$\overset{\frown}{CD}$的长.
]

答案:
1. (1)证明:
连接$BC$,$AD$。
在$\odot O$中,$\angle A$和$\angle D$所对的弧都是$\overset{\frown}{BC}$,根据同弧所对的圆周角相等,所以$\angle A=\angle D$。
已知$\angle A = \angle B$,则$\angle B=\angle D$。
因为$\angle BMC=\angle AMD$(对顶角相等),且$\angle B=\angle D$,$\angle A=\angle D$,$\angle A=\angle B$。
在$\triangle BMC$和$\triangle AMD$中,$\left\{\begin{array}{l}\angle B=\angle D\\\angle BMC=\angle AMD\\BC = AD\end{array}\right.$(同圆中,等圆周角所对的弦相等,$\angle A=\angle D$,所以$BC = AD$)。
根据$AAS$(两角及其中一角的对边对应相等)可得$\triangle BMC\cong\triangle AMD$。
所以$CM = DM$,$BM = AM$。
则$CM + AM=DM + BM$,即$AC = BD$。
2. (2)解:
连接$OC$,$OD$。
因为$\angle A = 30^{\circ}$,$\angle A=\angle D$(同弧所对圆周角相等),所以$\angle D = 30^{\circ}$。
又因为$AC\perp BD$,在$Rt\triangle ADM$中,$\angle A = 30^{\circ}$,$\angle AMD = 90^{\circ}$,则$\angle DAM=60^{\circ}$。
因为$OA = OC = OD = OB = 2$(半径)。
由$\angle A=\angle B = 30^{\circ}$,$\angle BOC = 2\angle A$(同弧所对圆心角是圆周角的$2$倍),$\angle AOD = 2\angle B$。
所以$\angle BOC=\angle AOD = 60^{\circ}$。
因为$\angle AOC+\angle AOD+\angle DOC+\angle BOC = 360^{\circ}$,且$\angle AOC=\angle BOD$($AC = BD$,等弦所对圆心角相等)。
又因为$\angle AOB=\angle AOC+\angle BOC$,$\angle AOB = 120^{\circ}$($\angle A = 30^{\circ}$,$\angle B = 30^{\circ}$,$\angle AOB=180^{\circ}-(\angle OAB+\angle OBA)=120^{\circ}$)。
所以$\angle DOC = 60^{\circ}$。
根据弧长公式$l=\frac{n\pi r}{180}$($n$是圆心角弧度数,$r$是半径),这里$n = 60$,$r = 2$。
则$\overset{\frown}{CD}$的长$l=\frac{60\pi×2}{180}=\frac{2\pi}{3}$。
综上,(1)得证$AC = BD$;(2)$\overset{\frown}{CD}$的长为$\frac{2\pi}{3}$。
连接$BC$,$AD$。
在$\odot O$中,$\angle A$和$\angle D$所对的弧都是$\overset{\frown}{BC}$,根据同弧所对的圆周角相等,所以$\angle A=\angle D$。
已知$\angle A = \angle B$,则$\angle B=\angle D$。
因为$\angle BMC=\angle AMD$(对顶角相等),且$\angle B=\angle D$,$\angle A=\angle D$,$\angle A=\angle B$。
在$\triangle BMC$和$\triangle AMD$中,$\left\{\begin{array}{l}\angle B=\angle D\\\angle BMC=\angle AMD\\BC = AD\end{array}\right.$(同圆中,等圆周角所对的弦相等,$\angle A=\angle D$,所以$BC = AD$)。
根据$AAS$(两角及其中一角的对边对应相等)可得$\triangle BMC\cong\triangle AMD$。
所以$CM = DM$,$BM = AM$。
则$CM + AM=DM + BM$,即$AC = BD$。
2. (2)解:
连接$OC$,$OD$。
因为$\angle A = 30^{\circ}$,$\angle A=\angle D$(同弧所对圆周角相等),所以$\angle D = 30^{\circ}$。
又因为$AC\perp BD$,在$Rt\triangle ADM$中,$\angle A = 30^{\circ}$,$\angle AMD = 90^{\circ}$,则$\angle DAM=60^{\circ}$。
因为$OA = OC = OD = OB = 2$(半径)。
由$\angle A=\angle B = 30^{\circ}$,$\angle BOC = 2\angle A$(同弧所对圆心角是圆周角的$2$倍),$\angle AOD = 2\angle B$。
所以$\angle BOC=\angle AOD = 60^{\circ}$。
因为$\angle AOC+\angle AOD+\angle DOC+\angle BOC = 360^{\circ}$,且$\angle AOC=\angle BOD$($AC = BD$,等弦所对圆心角相等)。
又因为$\angle AOB=\angle AOC+\angle BOC$,$\angle AOB = 120^{\circ}$($\angle A = 30^{\circ}$,$\angle B = 30^{\circ}$,$\angle AOB=180^{\circ}-(\angle OAB+\angle OBA)=120^{\circ}$)。
所以$\angle DOC = 60^{\circ}$。
根据弧长公式$l=\frac{n\pi r}{180}$($n$是圆心角弧度数,$r$是半径),这里$n = 60$,$r = 2$。
则$\overset{\frown}{CD}$的长$l=\frac{60\pi×2}{180}=\frac{2\pi}{3}$。
综上,(1)得证$AC = BD$;(2)$\overset{\frown}{CD}$的长为$\frac{2\pi}{3}$。
查看更多完整答案,请扫码查看


