7. 抛物线 $ y = ax^{2} + b $ 的图象如图所示,则下列结论中正确的是(
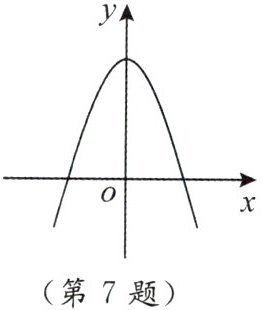
A.$ a > 0,b < 0 $
B.$ a > 0,b > 0 $
C.$ a < 0,b < 0 $
D.$ a < 0,b > 0 $
D
)
A.$ a > 0,b < 0 $
B.$ a > 0,b > 0 $
C.$ a < 0,b < 0 $
D.$ a < 0,b > 0 $
答案:
D
▲8. 若二次函数 $ y = ax^{2} + c(a \neq 0) $ 当 $ x $ 分别取 $ x_{1},x_{2}(x_{1} \neq x_{2}) $ 时,函数值相等,则当 $ x $ 取 $ x_{1} + x_{2} $ 时,函数值为(
A.$ a + b $
B.$ a - c $
C.$ c $
D.$ -c $
C
)A.$ a + b $
B.$ a - c $
C.$ c $
D.$ -c $
答案:
C
9. 抛物线向右平移 2 个单位,再向下平移 3 个单位得到 $ y = 2(x - 1)^{2} - 2 $,则原抛物线的函数表达式是
$y=2(x+1)^2+1$
.
答案:
$y=2(x+1)^2+1$
10. 抛物线 $ y = -(x - 2)^{2} - 1 $ 的顶点为 $ C $,直线 $ y = -2x + b $ 经过点 $ C $,且与 $ y $ 轴交于点 $ A $.求 $ \triangle OAC $ 的面积(点 $ O $ 为坐标原点).
答案:
3
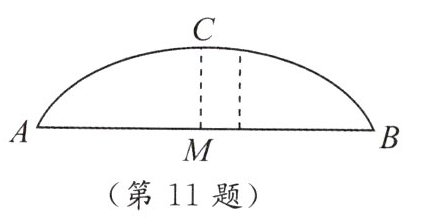
★11. 如图,一座拱桥呈抛物线状,桥的最大高度是 16 米,跨度为 40 米.请在图中建立以 $ AB $ 所在直线为 $ x $ 轴的平面直角坐标系,并使抛物线的顶点落在 $ y $ 轴正半轴上.
(1) 求该抛物线的函数表达式.
(2) 求在线段 $ AB $ 上离中心 $ M $ 处 5 米的地方桥的高度.
(1) 求该抛物线的函数表达式.
(2) 求在线段 $ AB $ 上离中心 $ M $ 处 5 米的地方桥的高度.

答案:
(1)$y=-\frac{1}{25}x^2+16$;
(2)15米。
(1)$y=-\frac{1}{25}x^2+16$;
(2)15米。
查看更多完整答案,请扫码查看


