《2025年全程助学与学习评估九年级数学上册浙教版》

1. “红灯停,绿灯行”是我们在日常生活中必须遵守的交通规则. 小刚每天从家骑自行车上学都经过三个路口,且每个路口只安装了红灯和绿灯,假如每个路口红灯和绿灯亮的时间相同,那么小刚从家随时出发去学校,他遇到两次红灯的概率是(B)
A.$\frac{1}{8}$
B.$\frac{3}{8}$
C.$\frac{5}{8}$
D.$\frac{7}{8}$

答案： B

2. 小明和小聪一起玩掷骰子游戏,规则如下：掷一次骰子,若骰子朝上一面的数字是6,则小聪胜；若骰子朝上一面的数字不是6,则小明胜. 你认为公平吗？

答案： 骰子共有6个面，数字1 - 6出现可能性相同，总共有6种等可能结果。
小聪胜的情况是骰子朝上一面数字为6，只有1种结果，所以小聪获胜的概率$P_1=\frac{1}{6}$。
小明胜的情况是骰子朝上一面数字不是6，有5种结果，所以小明获胜的概率$P_2=\frac{5}{6}$。
因为$\frac{1}{6}\neq\frac{5}{6}$，即两人获胜的概率不相等。
所以该游戏规则不公平。

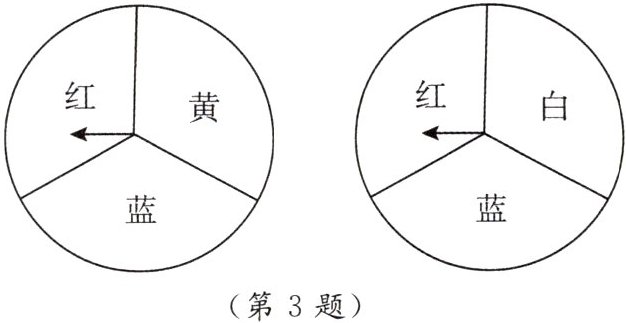
3. 游戏规则是：分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色. 此时小刚得1分,否则小明得1分. 这个游戏对双方公平吗？请说明理由. 若你认为不公平,如何修改规则才能使游戏对双方公平？

答案： 两个转盘均被分成面积相等的三个扇形区域，左边转盘分别标有红、蓝、黄，右边转盘分别标有红、蓝、白。
左边转盘转出红色的概率为$\frac{1}{3}$，转出蓝色的概率为$\frac{1}{3}$；
右边转盘转出红色的概率为$\frac{1}{3}$，转出蓝色的概率为$\frac{1}{3}$。
配成紫色的概率为左边转盘转出红色且右边转盘转出蓝色的概率加上左边转盘转出蓝色且右边转盘转出红色的概率，即：
$P(配成紫色)=\frac{1}{3} × \frac{1}{3} + \frac{1}{3} × \frac{1}{3} = \frac{2}{9}$。
$P(不配成紫色)=1 - \frac{2}{9} = \frac{7}{9}$。
小刚的得分期望为$\frac{2}{9} × 1 = \frac{2}{9}$，
小明的得分期望为$\frac{7}{9} × 1 = \frac{7}{9}$。
因为$\frac{2}{9} \lt \frac{7}{9}$，所以游戏不公平。
修改规则：若配成紫色，小刚得7分；否则小明得2分（答案不唯一，只要保证小刚和小明的得分期望相等即可）。