《2025年全程助学与学习评估九年级数学上册浙教版》

7. 一个点到圆上最近的点的距离是5,最远点的距离是11,则此圆的半径为3或8.

答案： 3或8

8. 已知$\odot O$的半径为2,点$P到圆心的距离OP = m$,且$m使关于x的二次方程2x^{2}-2\sqrt{2}x + m - 1 = 0$有实根,试确定点$P与\odot O$的位置关系.

答案： 要确定点$P$与$\odot O$的位置关系，需先求出$m$的取值范围，再比较$m$与圆半径$2$的大小。
步骤1：根据方程有实根求$m$的范围
对于二次方程$2x^2 - 2\sqrt{2}x + m - 1 = 0$，判别式$\Delta = b^2 - 4ac$。其中$a = 2$，$b = -2\sqrt{2}$，$c = m - 1$。
$\Delta = (-2\sqrt{2})^2 - 4 × 2 × (m - 1) = 8 - 8(m - 1) = 16 - 8m$。
方程有实根，则$\Delta \geq 0$，即$16 - 8m \geq 0$，解得$m \leq 2$。
步骤2：确定点$P$与$\odot O$的位置关系
$\odot O$的半径$r = 2$，点$P$到圆心的距离$OP = m$。
因为$m \leq 2$，所以：
当$m ＜ 2$时，点$P$在$\odot O$内；
当$m = 2$时，点$P$在$\odot O$上。
综上，点$P$在$\odot O$内或在$\odot O$上。
结论：点$P$在$\odot O$内或在$\odot O$上。

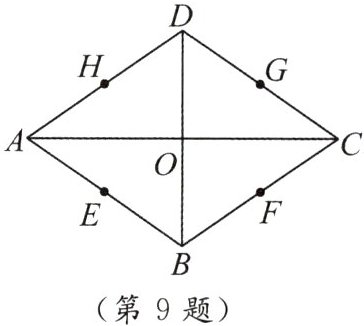
▲9. 如图,菱形$ABCD的对角线AC和BD相交于O$点,$E$,$F$,$G$,$H分别是AB$,$BC$,$CD$,$DA$的中点.求证：$E$,$F$,$G$,$H四点在以点O$为圆心的同一个圆上.

答案： 连接$OE$、$OF$、$OG$、$OH$。
因为四边形$ABCD$是菱形，
所以$AC\bot BD$，$AB = BC = CD = DA$，
点$O$是$ABCD$两对角线的中点。
因为$E$是$AB$的中点，
在$Rt\triangle AOB$中，$OE$为斜边$AB$上的中线，
所以$OE = \frac{1}{2}AB$。
同理可得$OF = \frac{1}{2}BC$，$OG = \frac{1}{2}CD$，$OH = \frac{1}{2}DA$。
因为$AB = BC = CD = DA$，
所以$OE = OF = OG = OH$。
即$E$、$F$、$G$、$H$四点在以$O$为圆心，以$\frac{1}{2}AB$为半径的圆上。

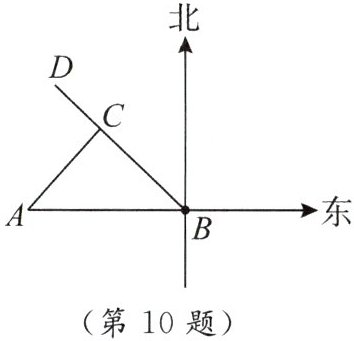
10. 由于过度采伐森林和破坏植被,我国某些地区经常受到沙尘暴的侵袭.$A市气象局测得沙尘暴中心在A市正东方向400\mathrm{km}的B$处,正在向西北方向转移(如图所示),距沙尘暴中心$300\mathrm{km}$的范围内将受到影响.$A$市是否会受到这次沙尘暴的影响？

答案： 过点$A$作$AC\perp BD$于点$C$。
在直角三角形$ABC$中，$\angle ABC = 45^{\circ}$，$AB = 400\mathrm{km}$。
根据三角函数$AC = AB\sin\angle ABC = 400×\frac{\sqrt{2}}{2}=200\sqrt{2}\approx200×1.414 = 282.8\mathrm{km}$。
因为$282.8\mathrm{km}\lt 300\mathrm{km}$。
所以$A$市会受到这次沙尘暴的影响。