6. 如图,二次函数 $ y = ax^{2} + bx + c $ 的图象开口向上,对称轴为直线 $ x = 1 $,图象经过点$(3,0)$,下列结论中,正确的一项是(
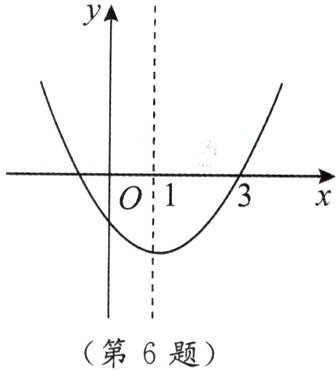
A.$ abc < 0 $
B.$ 2a + b < 0 $
C.$ a - b + c = 0 $
D.$ a + b + c > 0 $
C
)
A.$ abc < 0 $
B.$ 2a + b < 0 $
C.$ a - b + c = 0 $
D.$ a + b + c > 0 $
答案:
C
▲7. 若一次函数 $ y = ax + b $ 的图象经过第二、三、四象限,则二次函数 $ y = ax^{2} + bx $ 的图象只可能是(
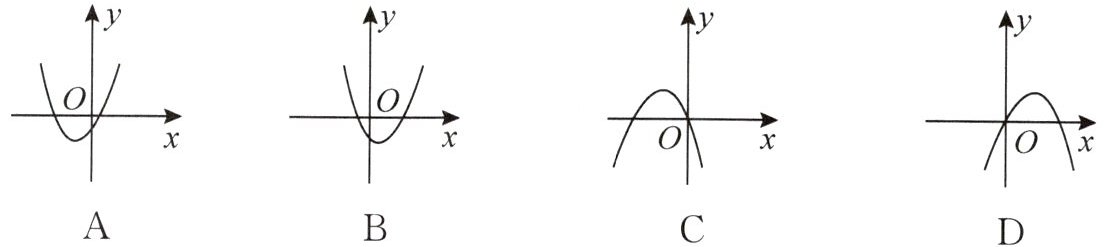
C
)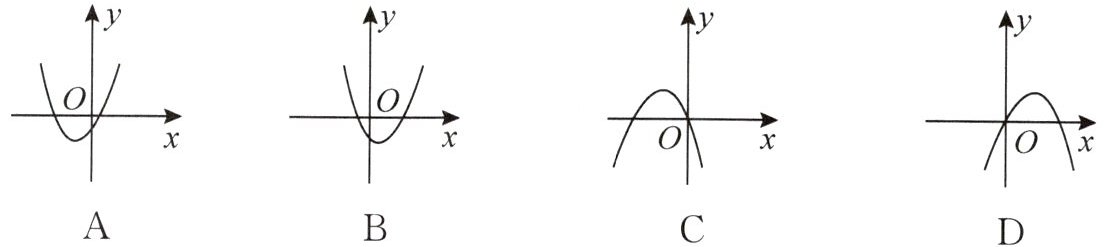
答案:
C
8. 二次函数 $ y = ax^{2} + bx + c $ 中,$ a > 0,b < 0,c < 0 $,则其图象的顶点是在第
四
象限.
答案:
四
9. 抛物线 $ y = \frac{1}{3}x^{2} - 2x - 5 $ 关于 $ y $ 轴对称的抛物线的函数表达式为
$y = \frac{1}{3}x^{2}+2x - 5$
.
答案:
$y = \frac{1}{3}x^{2}+2x - 5$
10. 若二次函数的图象对称轴是直线 $ x = \frac{3}{2} $,并且图象过 $ A(0,-4) $ 和 $ B(4,0) $.
(1) 求此二次函数图象上点 $ A $ 关于对称轴 $ x = \frac{3}{2} $ 对称的点 $ A' $ 的坐标.
(2) 求此二次函数的表达式.
(3) 画出这个二次函数的图象.
(1) 求此二次函数图象上点 $ A $ 关于对称轴 $ x = \frac{3}{2} $ 对称的点 $ A' $ 的坐标.
(2) 求此二次函数的表达式.
(3) 画出这个二次函数的图象.
答案:
(1)设点$A$关于对称轴$x = \frac{3}{2}$的对称点为$A^{\prime}(x,y)$。
由于点$A$和点$A^{\prime}$关于对称轴对称,所以它们的纵坐标相同,即$y = -4$。
点$A$和点$A^{\prime}$到对称轴的距离相等,所以$\frac{0 + x}{2} = \frac{3}{2}$,解得$x = 3$。
因此,点$A^{\prime}$的坐标为$(3, -4)$。
(2)设二次函数的表达式为$y = ax^{2} + bx + c$。
由于对称轴是$x = \frac{3}{2}$,所以$-\frac{b}{2a} = \frac{3}{2}$。
又因为函数图象过点$A(0, -4)$,所以$c = -4$。
将点$B(4, 0)$代入函数表达式,得到$16a + 4b - 4 = 0$。
解这个方程组:
$\begin{cases}-\frac{b}{2a} = \frac{3}{2}, \\16a + 4b - 4 = 0.\end{cases}$
得到$a = \frac{1}{2}$,$b = -\frac{3}{2}$。
因此,二次函数的表达式为$y = \frac{1}{2}x^{2} - \frac{3}{2}x - 4$。
(3)此题要求画出二次函数的图象,由于这是一个实际的绘图操作,无法用文字描述,故说明关键点:
列表:选取几个$x$值,计算出对应的$y$值,列出表格。
描点:在坐标系中描出这些点。
连线:用平滑的曲线连接这些点,得到二次函数的图象。
(图像为开口向上的抛物线,与y轴交点(0,-4),与x轴交点(-2,0),(4,0)等,顶点为(1.5,-6.125)在答题卡画出即可)
(1)设点$A$关于对称轴$x = \frac{3}{2}$的对称点为$A^{\prime}(x,y)$。
由于点$A$和点$A^{\prime}$关于对称轴对称,所以它们的纵坐标相同,即$y = -4$。
点$A$和点$A^{\prime}$到对称轴的距离相等,所以$\frac{0 + x}{2} = \frac{3}{2}$,解得$x = 3$。
因此,点$A^{\prime}$的坐标为$(3, -4)$。
(2)设二次函数的表达式为$y = ax^{2} + bx + c$。
由于对称轴是$x = \frac{3}{2}$,所以$-\frac{b}{2a} = \frac{3}{2}$。
又因为函数图象过点$A(0, -4)$,所以$c = -4$。
将点$B(4, 0)$代入函数表达式,得到$16a + 4b - 4 = 0$。
解这个方程组:
$\begin{cases}-\frac{b}{2a} = \frac{3}{2}, \\16a + 4b - 4 = 0.\end{cases}$
得到$a = \frac{1}{2}$,$b = -\frac{3}{2}$。
因此,二次函数的表达式为$y = \frac{1}{2}x^{2} - \frac{3}{2}x - 4$。
(3)此题要求画出二次函数的图象,由于这是一个实际的绘图操作,无法用文字描述,故说明关键点:
列表:选取几个$x$值,计算出对应的$y$值,列出表格。
描点:在坐标系中描出这些点。
连线:用平滑的曲线连接这些点,得到二次函数的图象。
(图像为开口向上的抛物线,与y轴交点(0,-4),与x轴交点(-2,0),(4,0)等,顶点为(1.5,-6.125)在答题卡画出即可)
查看更多完整答案,请扫码查看


