《2025年全程助学与学习评估九年级数学上册浙教版》

1. 函数 $ y = ax^{2} + bx + c $ 中,
(1) 二次项系数 $ a $,决定了它的图象的开口方向和大小.
(2) 一次项系数 $ b $ 与 $ a $ 一起决定了对称轴的位置,对称轴为直线 $x=-\frac{b}{2a}$.
(3) 常数项 $ c $：当 $ x = 0 $ 时,$y$的值为 $ c $,所以 $ c $ 决定了图象与 $ y $ 轴的交点坐标为$(0,c)$.

答案：
(1)方向；大小；
(2)直线 $x=-\frac{b}{2a}$；
(3)$y$；$(0,c)$

2. 函数 $ y = -x^{2} - 3x + 2 $ 的图象与 $ y $ 轴的交点坐标为(0,2).

答案： (0,2)

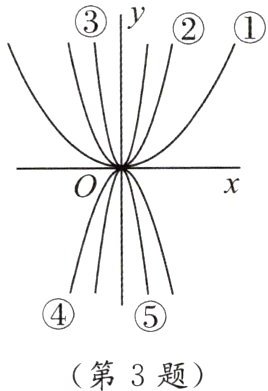
3. 如图,五条抛物线① $ y = a_{1}x^{2} $；② $ y = a_{2}x^{2} $；③ $ y = a_{3}x^{2} $；④ $ y = a_{4}x^{2} $；⑤ $ y = a_{5}x^{2} $.则 $ a_{1},a_{2},a_{3},a_{4},a_{5} $ 的大小关系是$a_{3}＜a_{4}＜a_{5}＜a_{1}＜a_{2}$(用“$＜$”连接).

答案： 【解析】：对于抛物线$y = ax^2$，$|a|$越大，抛物线开口越窄；$|a|$越小，抛物线开口越宽。由图可知，开口从宽到窄的顺序为：①、②、⑤、④、③。
①②开口向右，$a＞0$，开口越宽，$a$越小，所以$a_1 ＜ a_2$；
③④⑤开口向左，$a＜0$，开口越宽，$|a|$越小，即$a$越大（负数比较大小，绝对值大的反而小），所以$a_3 ＜ a_4 ＜ a_5$；
正数大于负数，故$a_3 ＜ a_4 ＜ a_5 ＜ a_1 ＜ a_2$。
【答案】：$a_{3}＜a_{4}＜a_{5}＜a_{1}＜a_{2}$

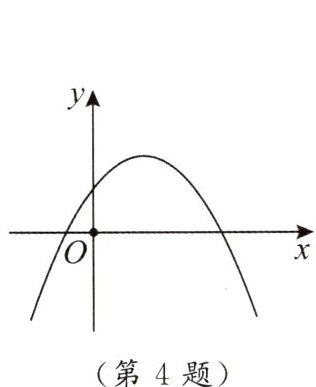
4. $ y = ax^{2} + bx + c $ 的图象如图,则 $ a,b,c $ 与 0 的大小关系是 $ a $＜0,$ b $＞0,$ c $＞0(用“$＜$”或“$＞$”连接).

答案： 【解析】：抛物线开口向下，所以 $a ＜ 0$；对称轴在 $y$ 轴右侧，即 $-\frac{b}{2a} ＞ 0$，又 $a ＜ 0$，所以 $b ＞ 0$；抛物线与 $y$ 轴交于正半轴，所以 $c ＞ 0$。
【答案】：＜，＞，＞

5. 已知函数 $ y = ax^{2} + bx + c $,当 $ x = -1 $ 时,$ y = 4 $,且图象经过点$(1,-4)$,$(0,-2)$.
(1) 求此函数表达式.
(2) 求它的对称轴和顶点坐标.

答案：
(1) 由题意得：
$\begin{cases}a(-1)^2 + b(-1) + c = 4 \\a(1)^2 + b(1) + c = -4 \\a(0)^2 + b(0) + c = -2\end{cases}$
即：
$\begin{cases}a - b + c = 4 \\a + b + c = -4 \\c = -2\end{cases}$
将$c = -2$代入前两式：
$\begin{cases}a - b - 2 = 4 \Rightarrow a - b = 6 \\a + b - 2 = -4 \Rightarrow a + b = -2\end{cases}$
两式相加：$2a = 4 \Rightarrow a = 2$，则$b = -2 - a = -4$
函数表达式为$y = 2x^2 - 4x - 2$
(2) 对称轴：$x = -\frac{b}{2a} = -\frac{-4}{2×2} = 1$
当$x = 1$时，$y = 2(1)^2 - 4(1) - 2 = -4$
顶点坐标为$(1, -4)$