《2025年全程助学与学习评估九年级数学上册浙教版》

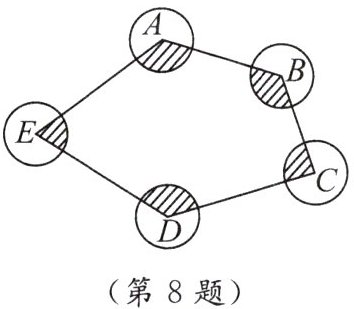
8. 如图,$\odot A$,$\odot B$,$\odot C$,$\odot D$,$\odot E半径都是1$,顺次连结五个圆心得到五边形$ABCDE$,则图中五个扇形(阴影部分)的面积之和是$\frac{3\pi}{2}$（或填$1.5\pi$）.
]

答案： $\frac{3\pi}{2}$（或填$1.5\pi$）

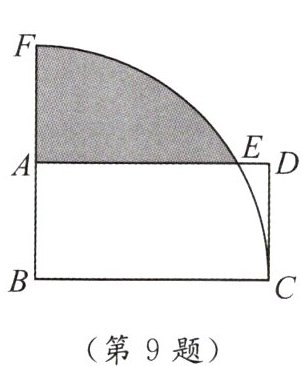
▲9. 如图,已知矩形$ABCD$中,$BC = 2AB$,以点$B$为圆心,$BC为半径的弧交AD于点E$,交$BA的延长线于点F$.设$AB = 1$,则阴影部分的面积为$\frac{2\pi}{3}-\frac{\sqrt{3}}{2}$.

答案： $\frac{2\pi}{3}-\frac{\sqrt{3}}{2}$

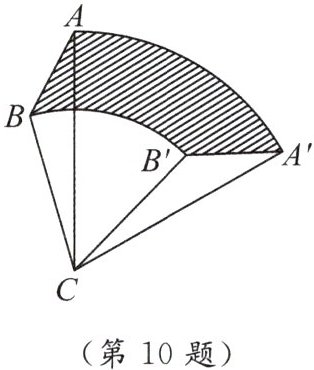
10. 如图,将$\triangle ABC绕点C旋转60^{\circ}得到\triangle A'B'C$,已知$AC = 6$,$BC = 4$,则线段$AB$扫过的图形面积为(D)

A.$\frac{3\pi}{2}$
B.$\frac{8\pi}{3}$
C.$6\pi$
D.$\frac{10\pi}{3}$

答案： D

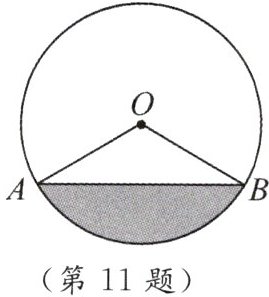
11. 如图,有一圆形的马戏帐篷,其半径为$20\mathrm{m}$,从点$A到点B$有一笔直的栅栏,$AB = 20\sqrt{3}\mathrm{m}$.
(1) 求$\angle AOB$的度数.
★(2) 某学校的学生在阴影区域里看马戏表演,已知每平方米中大约有$2$名学生,则该校大约有多少名学生在看戏？
]

答案：
(1) 由于 $OA = OB = 20\mathrm{m}$，$AB = 20\sqrt{3}\mathrm{m}$，
根据余弦定理，有：
$\ cos\angle AOB = \frac{OA^{2} + OB^{2} - AB^{2}}{2 × OA × OB} = \frac{20^{2} + 20^{2} - (20\sqrt{3})^{2}}{2 × 20 × 20} = -\frac{1}{2}$，
因为 $\angle AOB$ 在 $0°$ 到 $180°$ 之间，
所以 $\angle AOB = 120°$。
(2) 扇形的面积公式为：
$S = \frac{\theta}{360} × \pi r^{2}$，
其中 $\theta$ 是圆心角，$r$ 是半径。
将 $\theta = 120°$ 和 $r = 20\mathrm{m}$ 代入公式，得到：
$S_{扇形} = \frac{120}{360} × \pi × 20^{2} = \frac{400\pi}{3} \mathrm{m^2}$，
三角形 $AOB$ 的面积为：
$S_{\bigtriangleup AOB} = \frac{1}{2} × OA × OB × \ sin\angle AOB = \frac{1}{2} × 20 × 20 × \frac{\sqrt{3}}{2} = 100\sqrt{3}\mathrm{m^2}$，
阴影部分的面积为：
$S_{阴影} = S_{扇形} - S_{\bigtriangleup AOB} = (\frac{400\pi}{3} - 100\sqrt{3})\mathrm{m^2}$，
已知每平方米有 2 名学生，
所以学生总数为：
$2 × (\frac{400\pi}{3} - 100\sqrt{3}) \approx 2 × (418.88 - 173.2) = 491.36 \approx 491$（名），
（或写为$492$名，四舍五入不同）
答：该校大约有$491$（或$492$）名学生在看戏。