1. 若$△ABC\backsim △A'B'C'$,$BC=3$,$B'C'=1.8$,则$△A'B'C'$与$△ABC$的相似比为(
A.$5:3$
B.$3:2$
C.$2:3$
D.$3:5$
D
)A.$5:3$
B.$3:2$
C.$2:3$
D.$3:5$
答案:
D
2. 已知$△ABC\backsim △A'B'C'$,且相似比为$\frac{1}{3}$。若$A'B'=2$,则$AB=$
$\frac{2}{3}$
。
答案:
$\frac{2}{3}$
3. 如图,已知$△ADE\backsim △ACB$,且$∠ADE=∠C$,则$AD:AC=$(
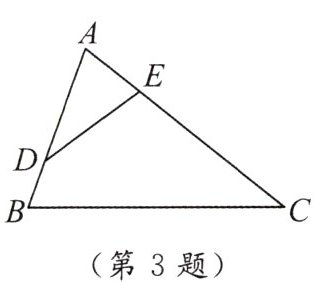
A.$AE:AC$
B.$DE:BC$
C.$AE:BC$
D.$DE:AB$
B
)
A.$AE:AC$
B.$DE:BC$
C.$AE:BC$
D.$DE:AB$
答案:
B
4. 如图,已知$△ADE\backsim △ABC$,其中$∠ADE=∠B$,则$\frac{AD}{AB}=$
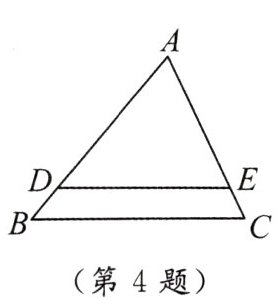
$\frac{AE}{AC}$
$=$$\frac{DE}{BC}$
。
答案:
$\frac{AE}{AC}$;$\frac{DE}{BC}$。
5. 如图,已知$△ABC\backsim △ACD$,则$\frac{AB}{AC}=$
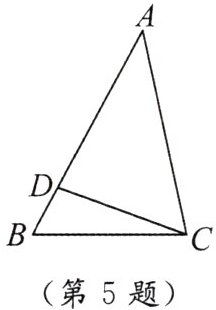
$\frac{AC}{AD}$
$=$$\frac{BC}{CD}$
。
答案:
$\frac{AC}{AD}$,$\frac{BC}{CD}$(答案写反不影响)。
6. 在$△ABC$中,$AB=5$,$BC=2\sqrt{6}$,$CA=3\sqrt{3}$,若$△ABC\backsim △A_1B_1C_1$,且$△A_1B_1C_1$的最长边长为$6\sqrt{6}$,则它的最短边长为
$8\sqrt{3}$
。
答案:
$8\sqrt{3}$
7. 如图,$BD// AC$,$AB$与$CD$相交于点$O$,$△OBD\backsim △OAC$,$\frac{OD}{OC}=\frac{2}{3}$,$OB=4$。求$AB$的长。
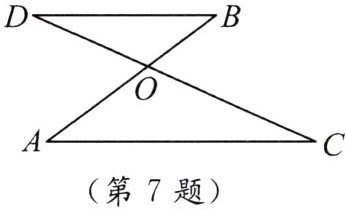

答案:
∵ $△OBD \backsim △OAC$,
$\therefore \frac{OB}{OA} = \frac{OD}{OC} = \frac{2}{3}$,
$\therefore \frac{4}{OA} = \frac{2}{3}$,
$\therefore OA = 6$,
$\therefore AB = OA + OB = 6 + 4 = 10$。
故$AB$的长为$10$。
∵ $△OBD \backsim △OAC$,
$\therefore \frac{OB}{OA} = \frac{OD}{OC} = \frac{2}{3}$,
$\therefore \frac{4}{OA} = \frac{2}{3}$,
$\therefore OA = 6$,
$\therefore AB = OA + OB = 6 + 4 = 10$。
故$AB$的长为$10$。
查看更多完整答案,请扫码查看


