1. 对于二次函数 $ y = - 5 x ^ { 2 } + 6 x - 1 $,下列说法中正确的是(
A.有最小值 $ 0.8 $
B.有最大值 $ 0.8 $
C.有最小值 $ - 2.8 $
D.有最大值 $ - 2.8 $
B
)A.有最小值 $ 0.8 $
B.有最大值 $ 0.8 $
C.有最小值 $ - 2.8 $
D.有最大值 $ - 2.8 $
答案:
B
2. 某公司准备修建一个长方体的污水处理池,池底矩形的周长为 $ 100 \mathrm { m } $,则池底的最大面积是(
A.$ 600 \mathrm { m } ^ { 2 } $
B.$ 625 \mathrm { m } ^ { 2 } $
C.$ 650 \mathrm { m } ^ { 2 } $
D.$ 675 \mathrm { m } ^ { 2 } $
B
)A.$ 600 \mathrm { m } ^ { 2 } $
B.$ 625 \mathrm { m } ^ { 2 } $
C.$ 650 \mathrm { m } ^ { 2 } $
D.$ 675 \mathrm { m } ^ { 2 } $
答案:
B
3. 二次函数 $ y = - \frac { 2 } { 3 } x ^ { 2 } + 4 x - 1 $,当 $ x = $
3
时,取到最大值.
答案:
3
4. 某学生推铅球,铅球飞行的高度 $ y ( \mathrm { m } ) $ 与水平距离 $ x ( \mathrm { m } ) $ 之间的函数表达式是 $ y = - \frac { 1 } { 32 } x ^ { 2 } + \frac { 1 } { 16 } x + \frac { 3 } { 2 } $,则铅球落地的水平距离为
8
$ \mathrm { m } $.
答案:
8
5. 已知当 $ x = 3 $ 时,二次函数有最大值 $ - 1 $,且图象与 $ y $ 轴交于点 $ ( 0, - 4 ) $,求该二次函数的表达式.
答案:
设二次函数的表达式为$y=a(x-h)^2+k$。
因为当$x = 3$时,二次函数有最大值$-1$,所以顶点坐标为$(3,-1)$,即$h=3$,$k=-1$,函数表达式为$y=a(x - 3)^2 - 1$。
又因为图象与$y$轴交于点$(0,-4)$,将$x=0$,$y=-4$代入表达式得:
$-4=a(0 - 3)^2 - 1$
$-4 = 9a - 1$
$9a = -3$
$a=-\dfrac{1}{3}$
所以二次函数的表达式为$y=-\dfrac{1}{3}(x - 3)^2 - 1$,展开得$y=-\dfrac{1}{3}x^2 + 2x - 4$。
结论:该二次函数的表达式为$y=-\dfrac{1}{3}x^2 + 2x - 4$。
因为当$x = 3$时,二次函数有最大值$-1$,所以顶点坐标为$(3,-1)$,即$h=3$,$k=-1$,函数表达式为$y=a(x - 3)^2 - 1$。
又因为图象与$y$轴交于点$(0,-4)$,将$x=0$,$y=-4$代入表达式得:
$-4=a(0 - 3)^2 - 1$
$-4 = 9a - 1$
$9a = -3$
$a=-\dfrac{1}{3}$
所以二次函数的表达式为$y=-\dfrac{1}{3}(x - 3)^2 - 1$,展开得$y=-\dfrac{1}{3}x^2 + 2x - 4$。
结论:该二次函数的表达式为$y=-\dfrac{1}{3}x^2 + 2x - 4$。
6. 已知二次函数的图象 $ ( 0 \leqslant x \leqslant 3 ) $ 如图所示,该函数在所给自变量取值范围内,下列说法正确的是(
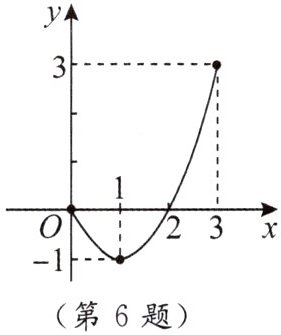
A.有最小值 $ 0 $,有最大值 $ 3 $
B.有最小值 $ - 1 $,有最大值 $ 0 $
C.有最小值 $ - 1 $,有最大值 $ 3 $
D.有最小值 $ - 1 $,无最大值
C
)
A.有最小值 $ 0 $,有最大值 $ 3 $
B.有最小值 $ - 1 $,有最大值 $ 0 $
C.有最小值 $ - 1 $,有最大值 $ 3 $
D.有最小值 $ - 1 $,无最大值
答案:
C
查看更多完整答案,请扫码查看


