《2025年全程助学与学习评估九年级数学上册浙教版》

7. 现已知线段 $ AB = 10 $,点 $ P $ 是线段 $ AB $ 的黄金分割点($ PA ＞ PB $),那么线段 $ PA $ 的长约为(C)
A.0.618
B.0.382
C.6.18
D.3.28

答案： C

8. 若 $ b $ 是 $ a $ 和 $ c $ 的比例中项,则关于 $ x $ 的一元二次方程 $ ax^2 + 2bx + c = 0 $ 的根的情况是(A)
A.有两个相等的实数根
B.有两个不相等的实数根
C.没有实数根
D.无法判断

答案： A

9. 已知线段 $ AB $ 及 $ AB $ 上一点 $ P $,当 $ P $ 满足下列哪一种关系时,$ P $ 为 $ AB $ 的黄金分割点：① $ AP^2 = AB \cdot PB $；② $ AP = \frac{\sqrt{5} - 1}{2}AB $；③ $ PB = \frac{3 - \sqrt{5}}{2}AB $；④ $ \frac{AP}{PB} = \frac{\sqrt{5} - 1}{2} $；⑤ $ \frac{AB}{AP} = \frac{\sqrt{5} - 1}{2} $. 其中正确的是(A)
A.①②③
B.①②③④
C.①②
D.①②③④⑤

答案： A

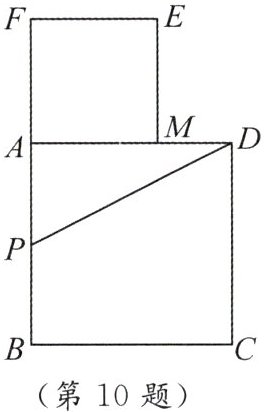
10. 如图,以长为 $ 2 $ 的线段 $ AB $ 为边作正方形 $ ABCD $,取 $ AB $ 的中点 $ P $,连结 $ PD $,在 $ BA $ 的延长线上取点 $ F $,使 $ PF = PD $,以 $ AF $ 为边作正方形 $ AMEF $,点 $ M $ 在 $ AD $ 上.
(1) 求 $ AM $,$ DM $ 的长.
(2) 求证：$ M $ 是线段 $ AD $ 的黄金分割点.

答案：
(1)
在$Rt\triangle APD$中，$AB = 2$，$P$为$AB$中点，则$AP=\frac{1}{2}AB = 1$，$AD = 2$。
根据勾股定理$PD=\sqrt{AP^{2}+AD^{2}}=\sqrt{1^{2}+2^{2}}=\sqrt{5}$。
因为$PF = PD=\sqrt{5}$，$AP = 1$，所以$AF=PF - AP=\sqrt{5}-1$。
因为四边形$AMEF$是正方形，所以$AM = AF=\sqrt{5}-1$。
$DM=AD - AM=2-(\sqrt{5}-1)=3 - \sqrt{5}$。
(2)
因为$AM=\sqrt{5}-1$，$AD = 2$，则$\frac{AM}{AD}=\frac{\sqrt{5}-1}{2}$。
由黄金分割点的定义可知，点$M$是线段$AD$的黄金分割点。
综上，答案为：
(1)$AM=\sqrt{5}-1$，$DM = 3-\sqrt{5}$；
(2)证明过程如上述所示。