1. 如图,在$\odot O$中,$AB$,$CD为\odot O$的两条弦,且$OE\perp AB于E$,$OF\perp CD于F$,且$OE = OF$。根据上述条件能推出
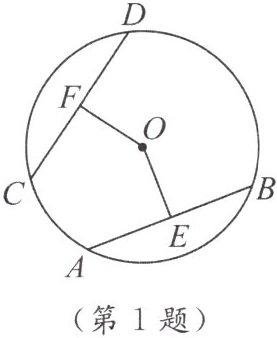
$AB=CD$,$\angle AOB=\angle COD$,$\overset{\frown}{AB}=\overset{\frown}{CD}$
(至少写三条)。
答案:
$AB=CD$,$\angle AOB=\angle COD$,$\overset{\frown}{AB}=\overset{\frown}{CD}$
2. 下列说法中,正确的是(
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
B
)A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
答案:
B
3. 如图,在$\odot O$中,$\overset{\frown}{AB}= 2\overset{\frown}{CD}$,那么(
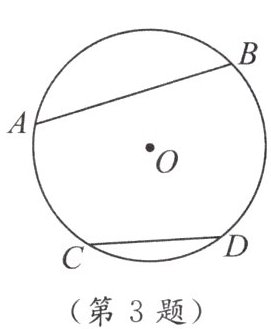
A.$AB>2CD$
B.$AB<2CD$
C.$AB = 2CD$
D.$AB与2CD$的大小无法比较
]
B
)
A.$AB>2CD$
B.$AB<2CD$
C.$AB = 2CD$
D.$AB与2CD$的大小无法比较
]
答案:
B
4. 如图,$AB是\overset{\frown}{AB}$所对的弦,$AB的中垂线CD分别交\overset{\frown}{AB}于C$,交$AB于D$,$AD的中垂线EF分别交\overset{\frown}{AB}于E$,交$AB于F$,$DB的中垂线GH分别交\overset{\frown}{AB}于G$,交$AB于H$,下列结论中不正确的是(
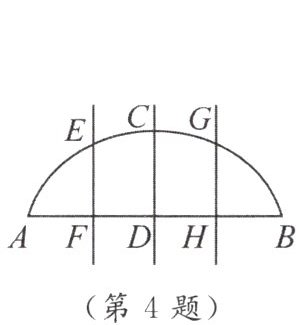
A.$\overset{\frown}{AC}= \overset{\frown}{CB}$
B.$\overset{\frown}{EC}= \overset{\frown}{CG}$
C.$\overset{\frown}{EC}= \overset{\frown}{AE}$
D.$EF = GH$
C
)
A.$\overset{\frown}{AC}= \overset{\frown}{CB}$
B.$\overset{\frown}{EC}= \overset{\frown}{CG}$
C.$\overset{\frown}{EC}= \overset{\frown}{AE}$
D.$EF = GH$
答案:
C
5. 如图,在$\odot O$中,弦$AB与弦CD$相交,且$AB = CD$。求证:$AC = BD$。
]
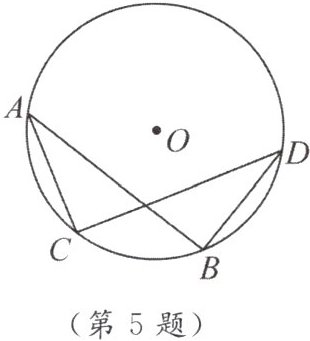
]

答案:
连接OA, OB, OC, OD。
∵AB=CD,OA=OB=OC=OD,
∴△OAB≌△OCD(SSS)。
∴∠AOB=∠COD。
∴∠AOB - ∠COB = ∠COD - ∠COB,即∠AOC=∠BOD。
∵OA=OC=OB=OD,∠AOC=∠BOD,
∴△AOC≌△BOD(SAS)。
∴AC=BD。
∵AB=CD,OA=OB=OC=OD,
∴△OAB≌△OCD(SSS)。
∴∠AOB=∠COD。
∴∠AOB - ∠COB = ∠COD - ∠COB,即∠AOC=∠BOD。
∵OA=OC=OB=OD,∠AOC=∠BOD,
∴△AOC≌△BOD(SAS)。
∴AC=BD。
查看更多完整答案,请扫码查看


