6. 一箱灯泡有 24 个,合格率为 80%,从中任拿一个是次品的概率为(
A.0.2
B.80%
C.$\frac{20}{24}$
D.1
A
)A.0.2
B.80%
C.$\frac{20}{24}$
D.1
答案:
A
7. 某射手在同一条件下进行射击,结果如下表所示:

请填写上表,由此表推断这个射手射击 1 次,击中靶心的概率的是

请填写上表,由此表推断这个射手射击 1 次,击中靶心的概率的是
0.9
.
答案:
1. 计算击中靶心频率:
当$n = 10$,$m = 8$时,$\frac{m}{n}=\frac{8}{10}=0.8$;
当$n = 20$,$m = 19$时,$\frac{m}{n}=\frac{19}{20}=0.95$;
当$n = 50$,$m = 44$时,$\frac{m}{n}=\frac{44}{50}=0.88$;
当$n = 100$,$m = 92$时,$\frac{m}{n}=\frac{92}{100}=0.92$;
当$n = 200$,$m = 178$时,$\frac{m}{n}=\frac{178}{200}=0.89$;
当$n = 500$,$m = 455$时,$\frac{m}{n}=\frac{455}{500}=0.91$。
2. 填表如下:
|射击次数$(n)$|10|20|50|100|200|500|…|
|----|----|----|----|----|----|----|----|
|击中靶心次数$(m)$|8|19|44|92|178|455|…|
|击中靶心频率$(\frac{m}{n})$|0.8|0.95|0.88|0.92|0.89|0.91|…|
3. 由上表推断这个射手射击 1 次,击中靶心的概率的是$0.9$。
当$n = 10$,$m = 8$时,$\frac{m}{n}=\frac{8}{10}=0.8$;
当$n = 20$,$m = 19$时,$\frac{m}{n}=\frac{19}{20}=0.95$;
当$n = 50$,$m = 44$时,$\frac{m}{n}=\frac{44}{50}=0.88$;
当$n = 100$,$m = 92$时,$\frac{m}{n}=\frac{92}{100}=0.92$;
当$n = 200$,$m = 178$时,$\frac{m}{n}=\frac{178}{200}=0.89$;
当$n = 500$,$m = 455$时,$\frac{m}{n}=\frac{455}{500}=0.91$。
2. 填表如下:
|射击次数$(n)$|10|20|50|100|200|500|…|
|----|----|----|----|----|----|----|----|
|击中靶心次数$(m)$|8|19|44|92|178|455|…|
|击中靶心频率$(\frac{m}{n})$|0.8|0.95|0.88|0.92|0.89|0.91|…|
3. 由上表推断这个射手射击 1 次,击中靶心的概率的是$0.9$。
8. 甲、乙、丙到操场上集合,甲希望自己能够排在第一位,如果排队次序由老师随机指定,那么愿望能够实现的概率为
$\frac{1}{3}$
.
答案:
$\frac{1}{3}$
9. 经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,那么三辆汽车经过这个十字路口,至少有两辆车向左转的概率为
$\frac{7}{27}$
.
答案:
$\frac{7}{27}$
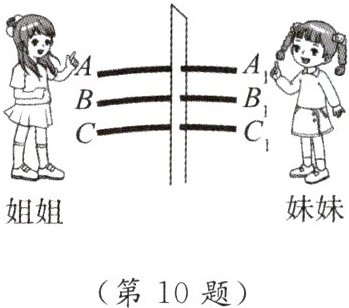
10. 如图,三根同样的绳子$AA_1$,$BB_1$,$CC_1$穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次两人各自选取本侧的一根绳子,每根绳子被选中的可能性相等.
(1)“姐妹两人同时选中同一根绳子”这一事件是
(2)在互相看不见的条件下,姐姐先将左侧 A,C 两个绳端打成一个结,妹妹从右侧$A_1$,$B_1$,$C_1$三个绳端中随机选两个打成一个结(打结后仍能自由地通过木孔). 请求出“姐姐抽动绳端 B,能抽出由三根绳子连结成的一根长绳”的概率是多少.
]
(1)“姐妹两人同时选中同一根绳子”这一事件是
随机
事件,概率是$\frac{1}{3}$
.(2)在互相看不见的条件下,姐姐先将左侧 A,C 两个绳端打成一个结,妹妹从右侧$A_1$,$B_1$,$C_1$三个绳端中随机选两个打成一个结(打结后仍能自由地通过木孔). 请求出“姐姐抽动绳端 B,能抽出由三根绳子连结成的一根长绳”的概率是多少.
]

$\frac{2}{3}$
答案:
(1) 随机;$\frac{1}{3}$;
(2) $\frac{2}{3}$
(1) 随机;$\frac{1}{3}$;
(2) $\frac{2}{3}$
查看更多完整答案,请扫码查看


