《2025年全程助学与学习评估九年级数学上册浙教版》

1. 已知二次函数 $ y= (m + 1)x^{m(m + 1)} $ 图象的开口向下,则 $ m $ 的值为(D)
A.$ 1 $
B.$ -1 $
C.$ 2 $
D.$ -2 $

答案： D

2. 函数 $ y = 3(x - 2)^2 + 1 $ 的图象向上平移 $ 2 $ 个单位,再向左平移 $ 2 $ 个单位所得图象的函数表达式为(A)
A.$ y = 3x^2 + 3 $
B.$ y = 3x^2 - 1 $
C.$ y = 3(x - 4)^2 + 3 $
D.$ y = 3(x - 4)^2 - 1 $

答案： A

3. 若二次函数 $ y = x^2 - 6x + c $ 的图象过 $ A(-1,y_1) $,$ B(2,y_2) $,$ C(3 + \sqrt{2},y_3) $,则 $ y_1 $,$ y_2 $,$ y_3 $ 的大小关系是$y_2\lt y_3\lt y_1$.

答案： $y_2\lt y_3\lt y_1$（按此顺序填写对应选项即可，假设选项顺序为$y_2\lt y_3\lt y_1$对应的选项）

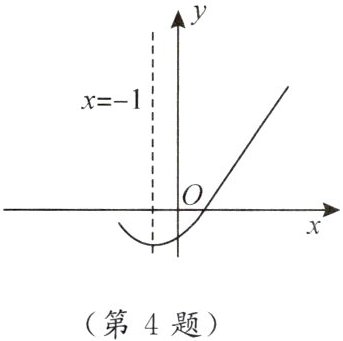
4. 如图是二次函数 $ y = ax^2 + bx + c(a \neq 0) $ 的图象的一部分,给出下列命题：① $ b^2 ＞ 4ac $；② $ abc ＞ 0 $；③ $ b ＞ 2a $；④ $ ax^2 + bx + c = 0 $ 的两根分别为 $ -3 $ 和 $ 1 $；⑤ $ 4a - 2b + c ＞ 0 $.其中正确的命题是①④(填写正确命题的序号).

答案： ①④

5. 已知二次函数 $ y = ax^2 + bx + c $ 中的 $ x $,$ y $ 满足下表.

求这个二次函数的表达式.

答案： 根据题意，可设二次函数的表达式为$y = ax^{2} + bx + c$。
把$( - 1,0)$，$(0, - 2)$，$(2,0)$代入$y = ax^{2} + bx + c$，
得$\begin{cases}a - b + c = 0,\\c = - 2,\\4a + 2b + c = 0.\end{cases}$
将$c = - 2$代入$a - b + c = 0$和$4a + 2b + c = 0$，
得$\begin{cases}a - b - 2 = 0,\\4a + 2b - 2 = 0.\end{cases}$
由$a - b - 2 = 0$可得$b = a - 2$，
将$b = a - 2$代入$4a + 2b - 2 = 0$，
得$4a + 2(a - 2) - 2 = 0$，
$4a + 2a - 4 - 2 = 0$，
$6a - 6 = 0$，
$6a = 6$，
解得$a = 1$。
把$a = 1$代入$b = a - 2$，
得$b = 1 - 2 = - 1$。
所以，二次函数表达式为$y = x^{2} - x - 2$。

6. 已知二次函数 $ y = -x^2 + 4x - 3 $.
(1) 写成 $ y = a(x - h)^2 + k $ 的形式,并指出函数图象的对称轴和顶点坐标.
(2) 求这个函数图象与坐标轴的交点坐标.

答案：
(1)
$y = -x^2 + 4x - 3$
$= - (x^2 - 4x + 4) + 1$
$= - (x - 2)^2 + 1$
对称轴为直线 $x = 2$；
顶点坐标为 $(2, 1)$。
(2)
当 $x = 0$ 时，$y = -3$，所以与 $y$ 轴交点坐标为 $(0, -3)$；
当 $y = 0$ 时，$-x^2 + 4x - 3 = 0$，
即$x^2 - 4x + 3 = 0$，
因式分解得$(x-1)(x-3)=0$
解得 $x_1 = 1$，$x_2 = 3$，
所以与 $x$ 轴交点坐标为 $(1, 0)$ 和 $(3, 0)$。