《2025年全程助学与学习评估九年级数学上册浙教版》

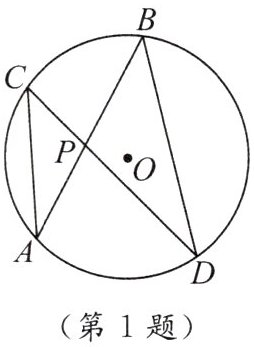
1. 如图,$\odot O$中,弦$AB$,$CD相交于点P$,若$\angle A= 30^{\circ}$,$\angle APD= 70^{\circ}$,则$\angle B= $40°.

答案： 40°

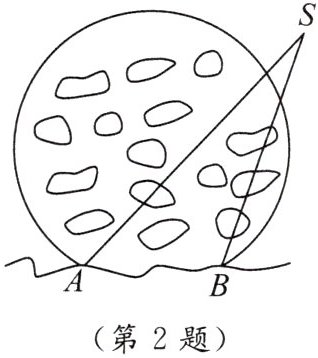
2. 如图,两灯塔$A$,$B$间的距离恰好为暗礁所在的圆的半径,要使船$S$不驶入暗礁区,则航行中应保持$\angle S$(D)

A.大于$60^{\circ}$
B.大于$30^{\circ}$
C.小于$60^{\circ}$
D.小于$30^{\circ}$

答案： 【解析】设暗礁所在圆的圆心为O，连接OA、OB。因为A、B间距离为圆的半径，所以OA=OB=AB，△OAB为等边三角形，∠AOB=60°。当船S在圆上时，∠ASB为弧AB所对圆周角，∠ASB=∠AOB/2=30°。船S不驶入暗礁区即S在圆外，此时∠ASB为圆外角，圆外角小于同弧所对圆周角，故∠ASB＜30°。
【答案】D

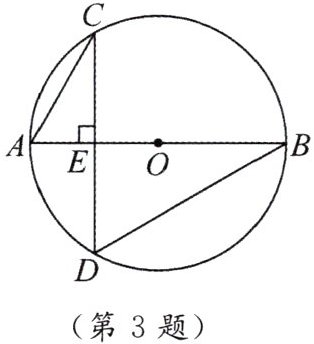
3. 如图,$AB是\odot O$的直径,弦$CD\perp AB于E$,$\angle ACD= 30^{\circ}$,$AE= 2cm$。求$DB$长。

答案： 连接OC，设⊙O的半径为r。
∵CD⊥AB于E，
∴∠AEC=90°。
在Rt△ACE中，∠ACD=30°，
∴∠CAE=60°，且AE=2cm。
∵∠ACD=30°，∠AEC=90°，
∴AC=2AE=4cm（30°角所对直角边是斜边一半）。
∵OA=OC=r，∠CAE=60°，
∴△OAC为等边三角形，
∴OA=AC=4cm，即r=4cm。
∴OE=OA-AE=4-2=2cm，AB=2r=8cm，EB=AB-AE=8-2=6cm。
∵CD⊥AB，由垂径定理得CE=DE。
在Rt△ACE中，CE=√(AC²-AE²)=√(4²-2²)=2√3 cm，
∴DE=2√3 cm。
在Rt△DEB中，DB=√(DE²+EB²)=√[(2√3)²+6²]=√(12+36)=√48=4√3 cm。
DB长为4√3 cm。

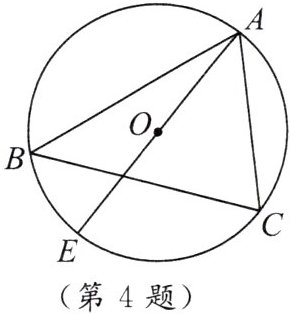
4. 如图,$\odot O的直径AE= 10cm$,$\angle B= \angle EAC$。求$AC$的长。

答案： 连接$EC$。
因为$AE$是$\odot O$的直径，
所以$\angle ACE = 90^{\circ}$（直径所对的圆周角是直角）。
因为$\angle B = \angle EAC$，$\angle E$与$\angle B$所对的弧都是$\overset{\frown}{AC}$，
所以$\angle E=\angle B$（同弧所对的圆周角相等），
所以$\angle E = \angle EAC$（等量代换）。
在$Rt\triangle AEC$中，$\angle E = \angle EAC$，
所以$AC = EC$（等角对等边）。
又因为$\angle ACE = 90^{\circ}$，根据勾股定理$AC^{2}+EC^{2}=AE^{2}$，
把$AC = EC$代入可得$2AC^{2}=AE^{2}$。
已知$AE = 10cm$，则$2AC^{2}=10^{2}=100$，
$AC^{2}=50$，
所以$AC = 5\sqrt{2}cm$。
综上，$AC$的长为$5\sqrt{2}cm$。