《2025年层层递进七年级数学上册苏科版》

17. (9 分)如图，已知点$E$在直线$AB$外，请使用三角板与直尺画图，并回答：
(1) 过点$E$作直线$CD$，使$CD//AB$；

(2) 过点$E$作直线$EF$，使$EF\perp AB$，垂足为$F$；
(3) 请判断直线$CD$与$EF$的位置关系，并说明理由.

答案：

(1) 
(2) 

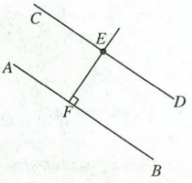
(3) CD⊥EF。理由：因为CD//AB，EF⊥AB，所以CD⊥EF（如果一条直线垂直于两条平行线中的一条，那么它也垂直于另一条）。

18. (8 分)如图，一个由 4 条线段构成的“鱼”形图案，其中$\angle 1 = 50^{\circ}$，$\angle 2 = 50^{\circ}$，$\angle 3 = 130^{\circ}$，找出图中的平行线，并说明理由.

答案： 解：$OA// BC$，$OB// AC$。
理由如下：
- 因为$\angle 1 = 50^{\circ}$，$\angle 2 = 50^{\circ}$，所以$\angle 1=\angle 2$。
根据“同位角相等，两直线平行”，可得$OB// AC$。
- 因为$\angle 2 = 50^{\circ}$，$\angle 3 = 130^{\circ}$，所以$\angle 2+\angle 3 = 50^{\circ}+130^{\circ}=180^{\circ}$。
根据“同旁内角互补，两直线平行”，可得$OA// BC$。
综上，图中的平行线为$OA// BC$，$OB// AC$。

19. (8 分)如图是一块四边形的铁砖的残余部分，量得$\angle A = 120^{\circ}$，$\angle B = 115^{\circ}$，且已知与$AB$平行的一条边部分破损，那么破损时的另外两个角分别是多少度?

答案： 19 60°和65°

20. (8 分)如图，点$O$在直线$AB$上，$OC$平分$\angle AOF$，$OD$平分$\angle BOF$，$F$是$DE$上一点，连接$OF$.
(1) 判断$OC$与$OD$是否垂直，并说明理由；

(2) 若$\angle D$与$\angle 1$互余，判断$ED$与$AB$是否平行，并说明理由.

答案： 1. （1）
解：$OC\perp OD$。
理由：因为$OC$平分$\angle AOF$，所以$\angle FOC = \frac{1}{2}\angle AOF$；因为$OD$平分$\angle BOF$，所以$\angle FOD=\frac{1}{2}\angle BOF$。
又因为$\angle AOF+\angle BOF = 180^{\circ}$（平角定义），所以$\angle COD=\angle FOC+\angle FOD=\frac{1}{2}(\angle AOF + \angle BOF)$。
把$\angle AOF+\angle BOF = 180^{\circ}$代入上式，得$\angle COD=\frac{1}{2}×180^{\circ}=90^{\circ}$，所以$OC\perp OD$。
2. （2）
解：$ED// AB$。
理由：因为$\angle D$与$\angle 1$互余，所以$\angle D+\angle 1 = 90^{\circ}$。
由（1）知$\angle COD = 90^{\circ}$，即$\angle 1+\angle FOD=90^{\circ}$，所以$\angle D=\angle FOD$（同角的余角相等）。
根据内错角相等，两直线平行，所以$ED// AB$。