《2025年层层递进七年级数学上册苏科版》

25. (6分)已知$A$，$B$两家销售公司员工工资的结算方式如下：$A$公司每月4000元基本工资，另加销售额的2％作为奖励性工资；$B$公司每月3600元基本工资，另加销售额的4％作为奖励性工资.已知$A$，$B$公司两位销售员小李、小张1～6月份的销售额如下表：

(1)小李1月份的工资是4180元，此时小张的工资是3980元；
(2)观察表格中数据的特点，若用$x$表示月份，则小李1～6月份的销售额用含$x$的代数式表示为$(2000x+7000)$元，小张1～6月份的销售额也用含$x$的代数式表示为$(1500x+8000)$元；
(3)如果7～12月份两人的销售额也分别满足(2)中的规律，试问到几月份小张的工资将追平小李的工资?

答案： 25.
(1)4180 3980
(2)$(2000x+7000)$ $(1500x+8000)$
(3)11月份

26. (6分)已知数轴上有$A$，$B$，$C$三点，分别表示有理数-26，-10，10，动点$P$从$A$出发，以每秒1个单位的速度向右移动，当$P$点运动到$C$点时运动停止，设

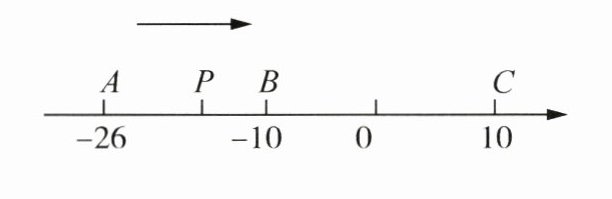
点

$P$

移

动

时

间

为

$t$

秒

.
(1)用含$t$的代数式表示$P$到点$A$和点$C$的距离：$PA=$$t$，$PC=$$36-t$.
(2)当点$P$运动到$B$点时，点$Q$从$A$出发，以每秒3个单位的速度向右运动，当点$Q$开始运动后.
①当$t=$$24$秒时，$P$，$Q$两点相遇；
②请用含$t$的代数式表示$P$，$Q$两点间的距离.(友情提醒：注意考虑$P$，$Q$的位置)

答案： 26.
(1)$t$ $36-t$
(2)①$t=24$ ②当$16\leq t\leq24$时,$PQ=48-2t$;当$24\leq t\leq36$时,$PQ=2t-48$