第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
22. (10分)【问题情景】
七(1)班综合实践小组进行废物再利用的环保小卫士行动,他们准备用废弃的宣传单制作装垃圾用的无盖纸盒.
【操作探究】
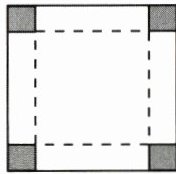
(1)若准备制作一个无盖的正方体纸盒,则下列

(2)如图,有一张边长为20 cm的正方形废弃宣传单,小明准备将其四角各剪去一个小正方形形,折成无盖长方体纸盒,若四角各剪去了一个边长为3 cm的小正方形,求这个纸盒的容积.
七(1)班综合实践小组进行废物再利用的环保小卫士行动,他们准备用废弃的宣传单制作装垃圾用的无盖纸盒.
【操作探究】
(1)若准备制作一个无盖的正方体纸盒,则下列
C
(填字母)图形经过折叠能围成无盖正方体纸盒.
(2)如图,有一张边长为20 cm的正方形废弃宣传单,小明准备将其四角各剪去一个小正方形形,折成无盖长方体纸盒,若四角各剪去了一个边长为3 cm的小正方形,求这个纸盒的容积.

答案:
1. (1)
答案:$C$。
2. (2)
解:
由题意可知,折成的无盖长方体纸盒底面是正方形,底面边长$a = 20−2×3$ $cm$,高$h = 3$ $cm$。
先计算底面边长:$a=20 - 6=14$ $cm$。
根据长方体容积公式$V=a× a× h$(这里$a$为底面边长,$h$为高)。
把$a = 14$ $cm$,$h = 3$ $cm$代入公式得:$V = 14×14×3$。
先计算$14×14=196$,再计算$196×3 = 588$($cm^{3}$)。
所以这个纸盒的容积是$588cm^{3}$。
答案:$C$。
2. (2)
解:
由题意可知,折成的无盖长方体纸盒底面是正方形,底面边长$a = 20−2×3$ $cm$,高$h = 3$ $cm$。
先计算底面边长:$a=20 - 6=14$ $cm$。
根据长方体容积公式$V=a× a× h$(这里$a$为底面边长,$h$为高)。
把$a = 14$ $cm$,$h = 3$ $cm$代入公式得:$V = 14×14×3$。
先计算$14×14=196$,再计算$196×3 = 588$($cm^{3}$)。
所以这个纸盒的容积是$588cm^{3}$。
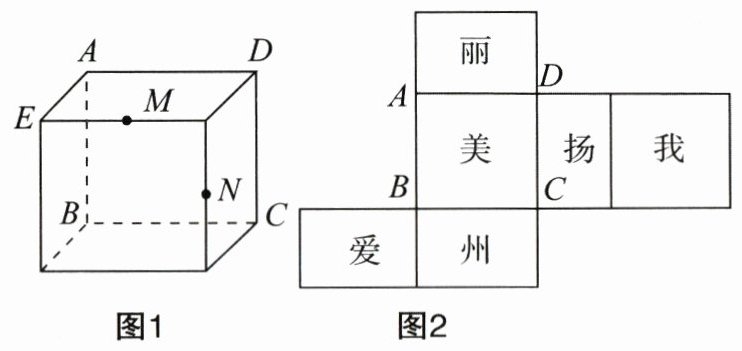
23. (12分)如图所示,图1为一个长方体,$AD=AB=10$,$AE=6$,图2为图1的表面展开图(字在外表面上),请根据要求回答问题:
(1)面“扬”的对面是面“
(2)如果面“丽”是右面,面“美”在后面,哪一面会在上面?
(3)图1中,$M$,$N$为所在棱的中点,试在图2中画出点$M$,$N$的位置,并求出图2中三角形$ABM$的面积(画出一种情况).
(1)面“扬”的对面是面“
爱
”;(2)如果面“丽”是右面,面“美”在后面,哪一面会在上面?
(3)图1中,$M$,$N$为所在棱的中点,试在图2中画出点$M$,$N$的位置,并求出图2中三角形$ABM$的面积(画出一种情况).

答案:
23.
(1)爱
(2)面“扬”
(3)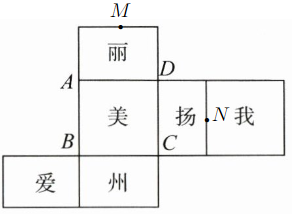 25(答案不唯一)
25(答案不唯一)
23.
(1)爱
(2)面“扬”
(3)
 25(答案不唯一)
25(答案不唯一) 查看更多完整答案,请扫码查看


