《2025年层层递进七年级数学上册苏科版》

25. (6 分)某商场对顾客实行优惠，规定:若一次购物不超过 200 元，则不予折扣;若一次购物超过 200 元，但不超过 500 元，按标价给予九折优惠;若一次购物超过 500 元，其中 500 元按九折优惠，超过 500 元的部分给予 8 折优惠，某人两次购物分别付款 168 元和 423 元，如果他合起来一次去购买同样的商品，他可节约多少钱?

答案： 25. 30.6元

26. (6 分)用如图所示大小完全相同的两个直角三角形纸片拼图，若将它们的某条边重合，能拼成几种不同形状的平面图形？先动手试一试，然后画出拼成的图形.

答案：
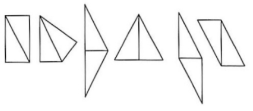
26. 

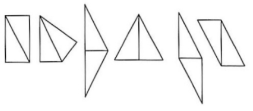
27. (6 分)12 人乘车去某地，可供租的车辆有两种:一种车可乘 8 人，另一种车可乘 4 人.
(1) 请给出 3 种租车方案；
(2) 如果第一种车的租金是 300 元/天，第二种车的租金是 200 元/天，那么采用哪种方案费用最少?

答案： 27.
(1) 方案一:8人座2辆,方案二:4人座3辆,方案三:8人座1辆和4人座1辆
(2) 8人座1辆和4人座1辆方案费用最少

28. (7 分)观察如图所示的图形，回答下列问题：

(1) 图中的点被线段隔开分成四层，第一层有 1 个点，第二层有 3 个点，第三层有 5 个点，第四层有7个点;
(2) 如果要你继续画下去，那么第五层有多少个点? 第 n 层呢?
(3) 某一层上有 77 个点，你知道这是第几层吗?
(4) 第一层与第二层的和是多少? 前三层的和是多少? 前四层呢? 你有没有发现什么规律(用含 n 的代数式表示)? 根据你的推测，前十二层的和是多少?

答案： 28.
(1) 7
(2) 第五层有9个点,第n层有(2n - 1)个点
(3) 第三十九层
(4) 第一层与第二层的和是4;前三层的和是9;前四层的和是16;前n层的和是n²;前十二层的和是144