第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
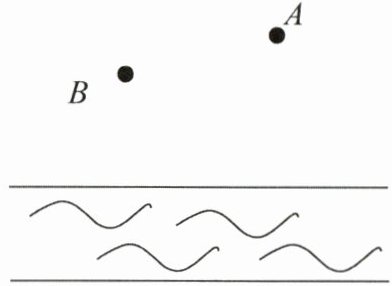
15. (8 分)如图,点$A$表示小明家,点$B$表示小明外婆家,若小明先去外婆家拿鱼具,然后再去河边钓鱼,怎样走路最短?请画出行走路径,并说明理由.

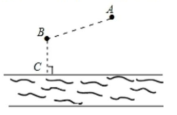
答案:
15.
15.

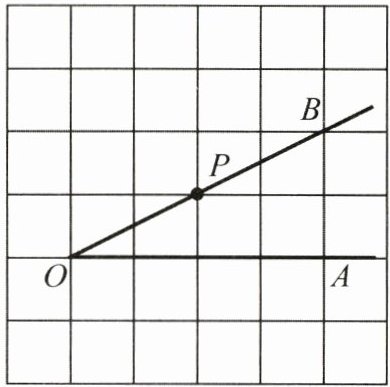
16. (7 分)如图,点$P$是$\angle AOB$的边$OB$上的一点.
(1) 过点$P$画$OB$的垂线,交$OA$于点$C$;
(2) 过点$P$画$OA$的垂线,垂足为点$H$;
(3) 线段$PH$的长度是点$P$到直线
(1) 过点$P$画$OB$的垂线,交$OA$于点$C$;
(2) 过点$P$画$OA$的垂线,垂足为点$H$;
(3) 线段$PH$的长度是点$P$到直线
$OA$
的距离,线段$CP$
的长度是点$C$到直线$OB$的距离,$PC$,$PH$,$OC$这三条线段的大小关系是$PH<PC<OC$
(用“$<$”连接).
答案:
16.
(1)
(2)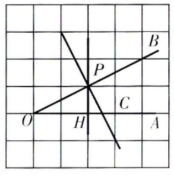
(3) $OA$ $CP$ $PH<PC<OC$
16.
(1)
(2)

(3) $OA$ $CP$ $PH<PC<OC$
17. (8 分)如图,所有小正方形的边长都为$1$,长方形的顶点都在格点上.请按要求解答:
(1) 画线段$AC$;
(2) 分别过点$D$,$B$作线段$AC$的垂线,垂足分别为点$E$,$F$;
(3) 因为
(4) 你能写出线段$DE$,$BF$的数量关系吗?(直接写出答案)
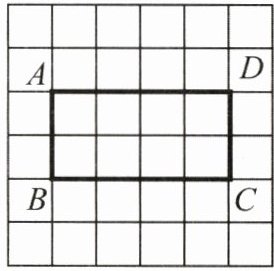
(1) 画线段$AC$;
(2) 分别过点$D$,$B$作线段$AC$的垂线,垂足分别为点$E$,$F$;
(3) 因为
略
,所以线段$AD$,$AE$的大小关系是$AE<AD$
(用“$<$”连接);(4) 你能写出线段$DE$,$BF$的数量关系吗?(直接写出答案)

答案:
17.
(1)
(2)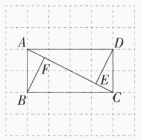
(3)$AE<AD$
(4)$DE=BF$
17.
(1)
(2)

(3)$AE<AD$
(4)$DE=BF$
18. (9 分)如图,直线$AB$与$CD$相交于点$O$,$OP$是$\angle BOC$的平分线,$OE\perp AB$,$OF\perp CD$.
(1) 如果$\angle AOD = 40^{\circ}$,
①那么根据
②$\angle POF$的度数是
(2) 图中除直角外,还有相等的角吗?请写出三对:
①
②
③
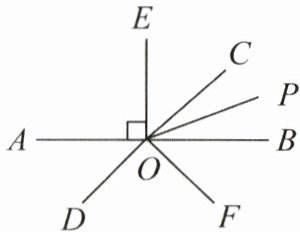
(1) 如果$\angle AOD = 40^{\circ}$,
①那么根据
对顶角相等
,可得$\angle BOC =$40
度;②$\angle POF$的度数是
70
度.(2) 图中除直角外,还有相等的角吗?请写出三对:
①
略
;②
略
;③
略
.
答案:
1. (1)
①
解:根据对顶角相等,因为$\angle AOD$与$\angle BOC$是对顶角,已知$\angle AOD = 40^{\circ}$,所以$\angle BOC=\angle AOD = 40^{\circ}$。
②
解:因为$OP$是$\angle BOC$的平分线,$\angle BOC = 40^{\circ}$,所以$\angle BOP=\angle POC=\frac{1}{2}\angle BOC=\frac{1}{2}×40^{\circ}=20^{\circ}$。
又因为$OF\perp CD$,所以$\angle COF = 90^{\circ}$。
则$\angle POF=\angle COF-\angle POC=90^{\circ}-20^{\circ}=70^{\circ}$。
2. (2)
①$\angle AOC=\angle BOD$(对顶角相等);
②$\angle EOC=\angle BOF$(因为$\angle EOC+\angle COB = 90^{\circ}$,$\angle BOF+\angle COB = 90^{\circ}$,同角的余角相等);
③$\angle EOB=\angle FOD$(因为$\angle EOB = 90^{\circ}$,$\angle FOD = 90^{\circ}$)。
故答案依次为:(1)①对顶角相等;$40$;②$70$;(2)①$\angle AOC=\angle BOD$;②$\angle EOC=\angle BOF$;③$\angle EOB=\angle FOD$(答案不唯一)。
①
解:根据对顶角相等,因为$\angle AOD$与$\angle BOC$是对顶角,已知$\angle AOD = 40^{\circ}$,所以$\angle BOC=\angle AOD = 40^{\circ}$。
②
解:因为$OP$是$\angle BOC$的平分线,$\angle BOC = 40^{\circ}$,所以$\angle BOP=\angle POC=\frac{1}{2}\angle BOC=\frac{1}{2}×40^{\circ}=20^{\circ}$。
又因为$OF\perp CD$,所以$\angle COF = 90^{\circ}$。
则$\angle POF=\angle COF-\angle POC=90^{\circ}-20^{\circ}=70^{\circ}$。
2. (2)
①$\angle AOC=\angle BOD$(对顶角相等);
②$\angle EOC=\angle BOF$(因为$\angle EOC+\angle COB = 90^{\circ}$,$\angle BOF+\angle COB = 90^{\circ}$,同角的余角相等);
③$\angle EOB=\angle FOD$(因为$\angle EOB = 90^{\circ}$,$\angle FOD = 90^{\circ}$)。
故答案依次为:(1)①对顶角相等;$40$;②$70$;(2)①$\angle AOC=\angle BOD$;②$\angle EOC=\angle BOF$;③$\angle EOB=\angle FOD$(答案不唯一)。
查看更多完整答案,请扫码查看


