第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
19. (8 分)如图,点$O$是直线$CE$上一点,以$O$为顶点作$\angle AOB = 90^{\circ}$,且$OA$,$OB$位于直线$CE$两侧,$OB$平分$\angle COD$.
(1) ①当$\angle AOC = 50^{\circ}$时,$\angle DOE$的度数为
②当$\angle AOC = 72^{\circ}$时,$\angle DOE$的度数为
(2) 通过(1)的计算,请你猜想$\angle AOC$和$\angle DOE$的数量关系,并说明理由.

(1) ①当$\angle AOC = 50^{\circ}$时,$\angle DOE$的度数为
$100°$
;②当$\angle AOC = 72^{\circ}$时,$\angle DOE$的度数为
$144°$
.(2) 通过(1)的计算,请你猜想$\angle AOC$和$\angle DOE$的数量关系,并说明理由.

答案:
1. 首先,根据已知条件进行分析:
因为$\angle AOB = 90^{\circ}$,$\angle AOC+\angle BOC = \angle AOB$,所以$\angle BOC=90^{\circ}-\angle AOC$。
又因为$OB$平分$\angle COD$,根据角平分线的定义,$\angle COD = 2\angle BOC$。
由于$\angle DOE+\angle COD = 180^{\circ}$(邻补角的定义:两角之和为$180^{\circ}$)。
2. 然后,推导$\angle AOC$与$\angle DOE$的关系:
把$\angle BOC = 90^{\circ}-\angle AOC$代入$\angle COD = 2\angle BOC$中,可得$\angle COD=2(90^{\circ}-\angle AOC)=180^{\circ}-2\angle AOC$。
再把$\angle COD = 180^{\circ}-2\angle AOC$代入$\angle DOE+\angle COD = 180^{\circ}$中,即$\angle DOE+(180^{\circ}-2\angle AOC)=180^{\circ}$。
对$\angle DOE+(180^{\circ}-2\angle AOC)=180^{\circ}$进行化简:
根据等式的性质,$\angle DOE+180^{\circ}-2\angle AOC = 180^{\circ}$。
等式两边同时减去$180^{\circ}$,得到$\angle DOE-2\angle AOC=0$。
所以$\angle DOE = 2\angle AOC$。
因为$\angle AOB = 90^{\circ}$,$\angle AOC+\angle BOC = \angle AOB$,所以$\angle BOC=90^{\circ}-\angle AOC$。
又因为$OB$平分$\angle COD$,根据角平分线的定义,$\angle COD = 2\angle BOC$。
由于$\angle DOE+\angle COD = 180^{\circ}$(邻补角的定义:两角之和为$180^{\circ}$)。
2. 然后,推导$\angle AOC$与$\angle DOE$的关系:
把$\angle BOC = 90^{\circ}-\angle AOC$代入$\angle COD = 2\angle BOC$中,可得$\angle COD=2(90^{\circ}-\angle AOC)=180^{\circ}-2\angle AOC$。
再把$\angle COD = 180^{\circ}-2\angle AOC$代入$\angle DOE+\angle COD = 180^{\circ}$中,即$\angle DOE+(180^{\circ}-2\angle AOC)=180^{\circ}$。
对$\angle DOE+(180^{\circ}-2\angle AOC)=180^{\circ}$进行化简:
根据等式的性质,$\angle DOE+180^{\circ}-2\angle AOC = 180^{\circ}$。
等式两边同时减去$180^{\circ}$,得到$\angle DOE-2\angle AOC=0$。
所以$\angle DOE = 2\angle AOC$。
20. (12 分)(1) 如图 1,在$3×3$的网格图中,标注了$6$个角,这些角中,有哪些互余的角?请分别写出来.
(2) 如图 2,在$5×5$的网格图中,标注了一些线段$AB$,$AI$,$CF$,$DF$,$EG$,$EI$,$CH$,$MH$,哪些线段是平行的?哪些线段是垂直的?请你分别写出来.
(3) 如图 3,在正方形网格中,小格的顶点叫作格点.小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连接三个格点,使之构成直角三角形,小华在左边的正方形网格中作出了$Rt\triangle ABC$.请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形各不相同.

(2) 如图 2,在$5×5$的网格图中,标注了一些线段$AB$,$AI$,$CF$,$DF$,$EG$,$EI$,$CH$,$MH$,哪些线段是平行的?哪些线段是垂直的?请你分别写出来.
(3) 如图 3,在正方形网格中,小格的顶点叫作格点.小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连接三个格点,使之构成直角三角形,小华在左边的正方形网格中作出了$Rt\triangle ABC$.请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形各不相同.

答案:
20.
(1) 根据全等的直角三角形可知∠1与∠6;∠2与∠5;∠3与∠4是互余的角;
(2) 根据正方形的性质,可知:平行的关系为:AB//EI、CF//MH、AJ//DF、EG//CH
(3) 如图所示:满足题意的直角三角形ABC,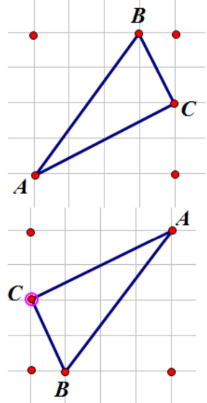
20.
(1) 根据全等的直角三角形可知∠1与∠6;∠2与∠5;∠3与∠4是互余的角;
(2) 根据正方形的性质,可知:平行的关系为:AB//EI、CF//MH、AJ//DF、EG//CH
垂直的关系为:AB⊥CF、EI⊥CF、AB⊥MH、EI⊥MH;
(3) 如图所示:满足题意的直角三角形ABC,

查看更多完整答案,请扫码查看


