《2025年云南省标准教辅同步指导训练与检测四年级数学上册人教版》

4. 不用测量,你知道∠2、∠3、∠4的大小吗？(3分)
已知∠1= 50°,那么∠2= (130°),∠3= (50°),∠4= (130°)。

答案： 解析：本题可根据平角的度数以及对顶角的性质来求解$\angle2$、$\angle3$、$\angle4$的度数。
步骤一：求$\angle2$的度数
观察图形可知，$\angle1$与$\angle2$组成一个平角，因为平角的度数是$180^{\circ}$，已知$\angle1 = 50^{\circ}$，所以根据平角的定义可得：
$\angle2=180^{\circ}-\angle1=180^{\circ}-50^{\circ}=130^{\circ}$
步骤二：求$\angle3$的度数
由对顶角的性质可知，对顶角相等。因为$\angle1$与$\angle3$是对顶角，所以$\angle3=\angle1 = 50^{\circ}$。
步骤三：求$\angle4$的度数
同样根据对顶角的性质，$\angle2$与$\angle4$是对顶角，所以$\angle4=\angle2 = 130^{\circ}$。
答案：$\angle2 = 130^{\circ}$，$\angle3 = 50^{\circ}$，$\angle4 = 130^{\circ}$。

1. 画一个75°的角。

答案：

2. 画一个150°的角。

答案：

1. 一个长方形花坛的长是250米,宽是80米,这个花坛的面积是多少平方米？合多少公顷？(4分)

答案： 长方形面积=长×宽
250×80=20000（平方米）
1公顷=10000平方米
20000平方米=2公顷
答：这个花坛的面积是20000平方米，合2公顷。

2.

磁悬浮列车 440千米/时 飞机的速度是磁悬浮列车的2倍
(1)磁悬浮列车12小时可以行驶多少千米？(4分)
(2)飞机从地球东半球某地起飞,飞至西半球某地要用15小时,你知道两地间的距离是多少千米吗？(4分)

答案：
(1)
解析：本题考查路程、速度、时间的关系，路程 = 速度×时间，已知磁悬浮列车速度和行驶时间，可求出行驶路程。
答案：$440×12 = 5280$（千米）
答：磁悬浮列车$12$小时可以行驶$5280$千米。
(2)
解析：先根据飞机速度与磁悬浮列车速度的倍数关系求出飞机速度，再根据路程 = 速度×时间，求出两地间的距离。
答案：飞机速度为$440×2 = 880$（千米/时）
$880×15 = 13200$（千米）
答：两地间的距离是$13200$千米。

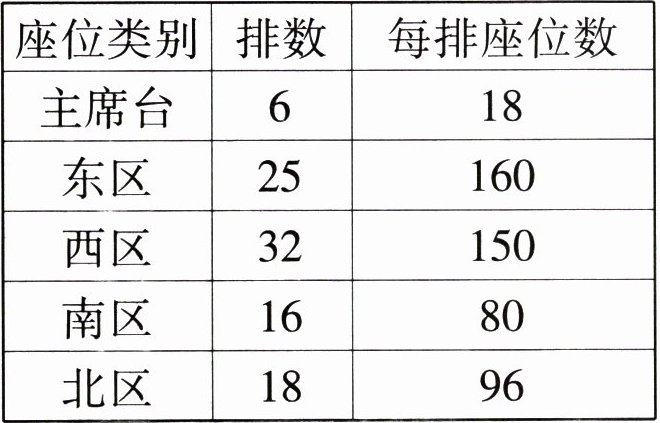
3. 右面是某体育场的座位情况。

(1)这个体育场可以容纳观众(11916)人。(2分)
(2)用“四舍五入”法保留到万位,这个体育场大约可以容纳观众(1万)人。(1分)

答案： 解析：本题考查的是利用乘法解决实际问题以及四舍五入法的运用。
先分别算出每个区域的座位数，再将所有区域的座位数相加，得到体育场可以容纳的总观众数。
主席台：$6 × 18 = 108$（个）；
东区：$25 × 160 = 4000$（个）；
西区：$32 × 150 = 4800$（个）；
南区：$16 × 80 = 1280$（个）；
北区：$18 × 96 = 1728$（个）。
总座位数：$108 + 4000 + 4800 + 1280 + 1728 = 11916$（个）。
用“四舍五入”法保留到万位，看千位上的数字，千位上是$1$，小于$5$，则万位上的数字不变，后面的数都变为$0$，所以$11916 \approx 10000$。
答案：
(1)$11916$；
(2)$1$万。