第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1.


|速度/(千米/时)|115|90|80|103|
| ---- | ---- | ---- | ---- | ---- |
|时间/时|16|4|5|26|
|路程/千米|1840|360|400|2678|
| ---- | ---- | ---- | ---- | ---- |
|时间/时|16|4|5|26|
|路程/千米|1840|360|400|2678|
答案:
解析:本题主要考查路程、速度和时间之间的关系,即$路程 = 速度×时间$,$速度 = 路程÷时间$,$时间 = 路程÷速度$。
第一列:已知速度为$115$千米/时,时间为$16$小时,根据上述公式可得路程为$115×16 = 1840$(千米)。
第二列:已知时间为$4$小时,路程为$360$千米,那么速度为$360÷4 = 90$(千米/时)。
第三列:已知速度为$80$千米/时,路程为$400$千米,所以时间为$400÷80 = 5$(小时)。
第四列:已知速度为$103$千米/时,时间为$26$小时,因此路程为$103×26 = 2678$(千米)。
答案:|速度/(千米/时)|115|90|80|103|
| ---- | ---- | ---- | ---- | ---- |
|时间/时|16|4|5|26|
|路程/千米|1840|360|400|2678|
第一列:已知速度为$115$千米/时,时间为$16$小时,根据上述公式可得路程为$115×16 = 1840$(千米)。
第二列:已知时间为$4$小时,路程为$360$千米,那么速度为$360÷4 = 90$(千米/时)。
第三列:已知速度为$80$千米/时,路程为$400$千米,所以时间为$400÷80 = 5$(小时)。
第四列:已知速度为$103$千米/时,时间为$26$小时,因此路程为$103×26 = 2678$(千米)。
答案:|速度/(千米/时)|115|90|80|103|
| ---- | ---- | ---- | ---- | ---- |
|时间/时|16|4|5|26|
|路程/千米|1840|360|400|2678|
2.

| 单价/元 | 78 | 2 | 6 | 83 |
| --- | --- | --- | --- | --- |
| 数量/件 | 36 | 18 | 30 | 270 |
| 总价/元 | 2808 | 36 | 180 | 22410 |

| 单价/元 | 78 | 2 | 6 | 83 |
| --- | --- | --- | --- | --- |
| 数量/件 | 36 | 18 | 30 | 270 |
| 总价/元 | 2808 | 36 | 180 | 22410 |
答案:
解析:本题主要考查了单价、数量和总价之间的关系,即总价 = 单价×数量,单价 = 总价÷数量,数量 = 总价÷单价。通过已知的单价和数量求出总价,已知总价和数量求出单价,已知总价和单价求出数量。
答案:
| 单价/元 | 78 | 2 | 6 | 83 |
| --- | --- | --- | --- | --- |
| 数量/件 | 36 | 18 | 30 | 270 |
| 总价/元 | 2808 | 36 | 180 | 22410 |
计算过程:
$78×36 = 2808$(元)
$36÷18 = 2$(元)
$180÷6 = 30$(件)
$83×270 = 22410$(元)
答案:
| 单价/元 | 78 | 2 | 6 | 83 |
| --- | --- | --- | --- | --- |
| 数量/件 | 36 | 18 | 30 | 270 |
| 总价/元 | 2808 | 36 | 180 | 22410 |
计算过程:
$78×36 = 2808$(元)
$36÷18 = 2$(元)
$180÷6 = 30$(件)
$83×270 = 22410$(元)
1. 买3台加湿器要804元,买6台同样的加湿器要多少钱?
答案:
解析:本题可先根据“总价÷数量 = 单价”求出每台加湿器的价格,再根据“单价×数量 = 总价”求出买$6$台加湿器的价格;也可根据倍数关系,$6$台是$3$台的$2$倍,那么买$6$台加湿器的价格就是买$3$台加湿器价格的$2$倍。
方法一:先求单价,再求总价
步骤一:计算每台加湿器的价格
已知买$3$台加湿器要$804$元,根据“总价÷数量 = 单价”,可得每台加湿器的价格为$804÷3 = 268$(元)。
步骤二:计算买$6$台加湿器的价格
根据“单价×数量 = 总价”,每台加湿器$268$元,买$6$台,可得买$6$台加湿器需要$268×6 = 1608$(元)。
方法二:根据倍数关系计算
因为$6÷3 = 2$,即$6$台是$3$台的$2$倍,那么买$6$台加湿器的价格就是买$3$台加湿器价格的$2$倍。
已知买$3$台加湿器要$804$元,所以买$6$台加湿器需要$804×2 = 1608$(元)。
答案:$1608$元。
方法一:先求单价,再求总价
步骤一:计算每台加湿器的价格
已知买$3$台加湿器要$804$元,根据“总价÷数量 = 单价”,可得每台加湿器的价格为$804÷3 = 268$(元)。
步骤二:计算买$6$台加湿器的价格
根据“单价×数量 = 总价”,每台加湿器$268$元,买$6$台,可得买$6$台加湿器需要$268×6 = 1608$(元)。
方法二:根据倍数关系计算
因为$6÷3 = 2$,即$6$台是$3$台的$2$倍,那么买$6$台加湿器的价格就是买$3$台加湿器价格的$2$倍。
已知买$3$台加湿器要$804$元,所以买$6$台加湿器需要$804×2 = 1608$(元)。
答案:$1608$元。
2. 王叔叔从工厂运货到外地,去时平均每小时行驶80千米,花了6小时送到。原路返回时,空车5小时就回到了工厂。返回时平均每小时行驶多少千米?
答案:
解析:本题考查的是路程、速度、时间的关系。路程、速度、时间的关系为:$路程=速度 × 时间$。
去时平均每小时行驶80千米,花了6小时送到,根据路程、速度、时间的关系,可以求出王叔叔从工厂到外地的路程为:
$80 × 6=480(千米)$。
原路返回时,空车5小时就回到了工厂,根据$速度=路程 ÷ 时间$,可以求出返回时平均每小时行驶:
$480 ÷ 5=96(千米)$。
答案:$80 × 6 ÷ 5=96(千米)$。
答:返回时平均每小时行驶96千米。
去时平均每小时行驶80千米,花了6小时送到,根据路程、速度、时间的关系,可以求出王叔叔从工厂到外地的路程为:
$80 × 6=480(千米)$。
原路返回时,空车5小时就回到了工厂,根据$速度=路程 ÷ 时间$,可以求出返回时平均每小时行驶:
$480 ÷ 5=96(千米)$。
答案:$80 × 6 ÷ 5=96(千米)$。
答:返回时平均每小时行驶96千米。
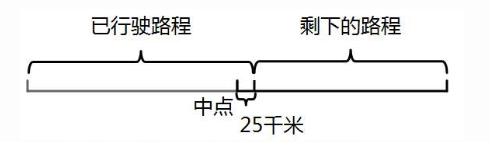
3. 国庆节期间,王叔叔自驾去北京游玩。汽车每小时行驶72千米,行驶6小时后,剩下的路程比全程的一半少25千米。王叔叔全程要行驶多少千米?(先画图再解答。)
答案:
解析:本题考查的是利用列方程来解决实际问题。
设王叔叔全程要行驶x千米。
那么全程的一半即($\frac{x}{2}$)千米。
已知汽车每小时行驶72千米,行驶了6小时,
则已经行驶的路程为($72 × 6$)千米。
剩下的路程比全程的一半少25千米,即($\frac{x}{2} - 25$)千米。
根据全程距离 - 剩下的路程 = 6小时行驶的路程,可以列出方程:
$x - (\frac{x}{2} - 25) = 72 × 6$
解这个方程:
去括号得:$x - \frac{x}{2}+ 25 = 432$。
合并同类项得:$\frac{x}{2}+ 25 = 432$。
等式两边同时减去25得:$\frac{x}{2}=407$。
系数化1得:$x=814$。
所以,王叔叔全程要行驶814千米。

解析:本题考查的是利用列方程来解决实际问题。
设王叔叔全程要行驶x千米。
那么全程的一半即($\frac{x}{2}$)千米。
已知汽车每小时行驶72千米,行驶了6小时,
则已经行驶的路程为($72 × 6$)千米。
剩下的路程比全程的一半少25千米,即($\frac{x}{2} - 25$)千米。
根据全程距离 - 剩下的路程 = 6小时行驶的路程,可以列出方程:
$x - (\frac{x}{2} - 25) = 72 × 6$
解这个方程:
去括号得:$x - \frac{x}{2}+ 25 = 432$。
合并同类项得:$\frac{x}{2}+ 25 = 432$。
等式两边同时减去25得:$\frac{x}{2}=407$。
系数化1得:$x=814$。
所以,王叔叔全程要行驶814千米。
数学小博士(附加题)
甲、乙两车同时从甲地出发开往乙地,甲车每小时行驶75千米,乙车每小时行驶55千米,多少小时后两车相距140千米?
甲、乙两车同时从甲地出发开往乙地,甲车每小时行驶75千米,乙车每小时行驶55千米,多少小时后两车相距140千米?
答案:
解析:本题可根据两车的速度差以及它们相距的路程,结合追及问题的基本公式来求解时间。
两车同时同地同向行驶,甲车速度比乙车速度快,随着时间的推移,两车的距离会逐渐拉开,两车的速度差为:$75 - 55 = 20$(千米/小时),而最终两车相距$140$千米,根据公式$时间 = 路程差÷速度差$,可求出行驶时间。
答案:
$140÷(75 - 55)$
$= 140÷20$
$= 7$(小时)
答:$7$小时后两车相距$140$千米。
两车同时同地同向行驶,甲车速度比乙车速度快,随着时间的推移,两车的距离会逐渐拉开,两车的速度差为:$75 - 55 = 20$(千米/小时),而最终两车相距$140$千米,根据公式$时间 = 路程差÷速度差$,可求出行驶时间。
答案:
$140÷(75 - 55)$
$= 140÷20$
$= 7$(小时)
答:$7$小时后两车相距$140$千米。
查看更多完整答案,请扫码查看


