《2025年云南省标准教辅同步指导训练与检测四年级数学上册人教版》

2. 下午3:15时,钟面上的时针和分针的夹角是(A)。
A.锐角
B.直角
C.钝角

答案： 解析：本题考查钟面角的知识，涉及到时针与分针在钟面上的位置关系以及角的分类。
我们知道一圈为$360^{\circ}$，分针每小时转一圈，也就是$60$分钟转$360^{\circ}$，所以分针每分钟转的角度为：$360÷60 = 6^{\circ}$。
时针每$12$小时转一圈，那么时针每小时转的角度为$360÷12 = 30^{\circ}$，所以时针每分钟转的角度为$30÷60 = 0.5^{\circ}$。
下午$3:15$时，分针指向$3$，走了$15$分钟，根据分针每分钟转$6^{\circ}$，可得此时分针走了$15×6^{\circ}= 90^{\circ}$。
时针在$3$点的位置基础上又走了$15$分钟，$3$点时，时针指向$3$，此时时针与分针夹角为$90^{\circ}$，$15$分钟时针又走了$15×0.5^{\circ}= 7.5^{\circ}$，那么此时时针与分针的夹角是$90^{\circ}-7.5^{\circ}= 77.5^{\circ}$。
根据角的分类，大于$0^{\circ}$而小于$90^{\circ}$的角是锐角，$77.5^{\circ}$在这个范围内，所以这个角是锐角。
答案：A。

四、解决问题。
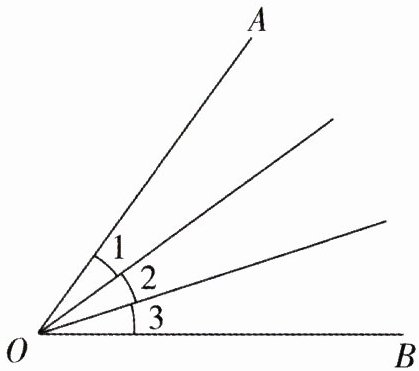
如下图所示,∠1= ∠2= ∠3。如果图中所有角的度数之和是180°,那么∠AOB是多少度？

答案： 设∠1=∠2=∠3=x°。
图中角有：∠1，∠2，∠3，∠1+∠2，∠2+∠3，∠1+∠2+∠3。
所有角的度数之和为：x + x + x + (x+x) + (x+x) + (x+x+x) = 10x。
10x = 180，x = 18。
∠AOB = ∠1+∠2+∠3 = 3x = 3×18 = 54°。
答：∠AOB是54度。

1.
∠1= 39° ∠2= ( )°

答案： 51

∠1= 120° ∠2= (60)°
∠3= (120)° ∠4= (60)°

答案： 60;120;60

3. 下面两幅图都是用一副三角尺拼成的。∠1、∠2各是多少度？

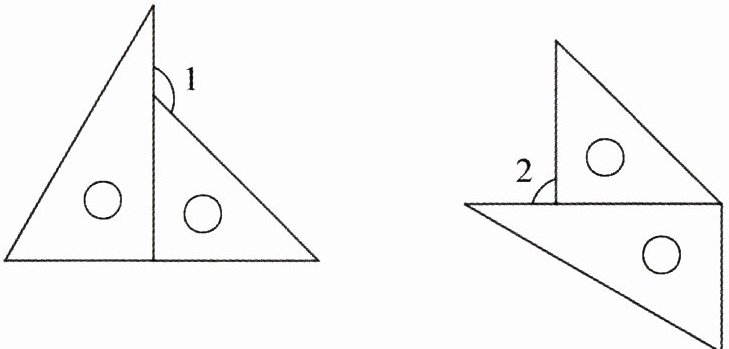
答案： ∠1=180°-45°=135°
∠2=90°