《2025年畅响假期衔接优化作业八年级数学华师大版》

1. 已知一次函数$y= kx+b(k≠0)$,在$-3≤x≤2的范围内y$的最大值比最小值大5,则下列说法正确的是(A)
A.$k$的值为1或-1
B.$y随x$增大而减小
C.该函数图象不可能经过一、二、四象限
D.满足题意的函数表达式只有2个

答案： A

2. 如图,等腰直角三角形$\triangle OAB的边OA和矩形OCDE的边OC在x$轴上,$OA= 4$,$OC= 1$,$OE= 2$。将矩形$OCDE沿x轴正方向平移t(t＞0)$个单位,所得矩形与$\triangle OAB公共部分的面积记为S(t)$。将$S(t)看作t$的函数,当自变量$t$在下列哪个范围取值时,$S(t)是t$的一次函数(D)
A.$1＜t＜2$
B.$2＜t＜3$
C.$3＜t＜4$
D.$1＜t＜2或4＜t＜5$

答案： D

3. 已知一次函数$y= kx+b(k≠0)$的图象经过点A(3,0),与$y轴交于点B$,$O$为坐标原点,若$\triangle AOB$的面积为6,则该一次函数的表达式为(B)
A.$y= -\frac{3}{4}x+4或y= \frac{3}{4}x-4$
B.$y= -\frac{4}{3}x+4或y= \frac{4}{3}x-4$
C.$y= -\frac{4}{3}x+4或y= \frac{4}{3}x+4$
D.$y= -\frac{4}{3}x-4或y= \frac{4}{3}x+4$

答案： B

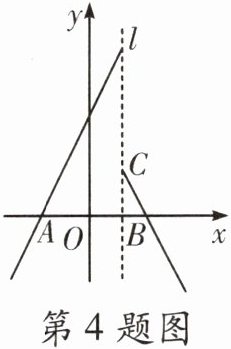
4. 定义图象与$x轴有两个交点的函数y= \begin{cases}-2x+4(x≥m)\\2x+4(x＜m)\end{cases} $,叫做关于直线$x= m$的对称函数,它与$x轴负半轴的交点记为A$,与$x轴正半轴的交点记为B$。例如,如图：直线$l:x= 1$,关于直线$l的对称函数y= \begin{cases}-2x+4(x≥1)\\2x+4(x＜1)\end{cases} $,与该直线$l交于点C$,当直线$y= x与关于直线x= m$的对称函数有两个交点时,则$m$的取值范围是(B)


A.$0≤m≤\frac{4}{3}$
B.$-2＜m≤\frac{4}{3}$
C.$-2＜m≤2$
D.$-4＜m＜0$

答案： B

5. 若关于$x的函数y= kx^{-2k+3}-x+5$是一次函数,则$k=$0或$\frac{3}{2}$。

答案： 0或$\frac{3}{2}$

6. 已知点$A(a,y_1)$、$B(a+1,y_2)在反比例函数y= \frac{-m^2-1}{x}$($m$是常数)的图象上,且$y_1＞y_2$,则$a$的取值范围是$-1 ＜ a ＜ 0$。

答案： $-1 ＜ a ＜ 0$

7. 如图,在平面直角坐标系中有两条直线$l_1:y= \frac{3}{4}x+3$,$l_2:y= -3x+3$,则$AB与AC$的数量关系为$AB = AC$,若$l_2上的一点M到l_1$的距离是2,则点$M$的坐标为$(\frac{2}{3},1)$或$(-\frac{2}{3},5)$。

答案： $AB = AC$，$(\frac{2}{3},1)$或$(-\frac{2}{3},5)$

8. 一个有进水管与出水管的容器,从某时刻开始的3分钟内只进水不出水,在随后的9分钟内既进水又出水,每分钟的进水量和出水量都是常数。容器内的水量$y$(升)与时间$x$(分钟)之间的关系如图所示。当容器内的水量大于5升时,时间$x$的取值范围为$1 ＜ x ＜ 9$。

答案： $1 ＜ x ＜ 9$

9. 为迎接中招体育考试,某校决定采购一批足球以供学生业余训练使用。某体育用品超市推出以下两种优惠方案：方案一,一律打八折；方案二,当购买量不超过80个时,按原价销售,当购买量超过80个时,超过的部分打六折。已知一个足球的原价为50元,设学校计划购买$x$个足球。
(1)设方案一的总费用为$y_1$,方案二的总费用为$y_2$,请分别写出$y_1$、$y_2$(元)与$x$(个)之间的函数关系式。
(2)若派学生代表去采购足球,他们应该选择哪种方案更省钱？并说明理由。

答案： 解:
(1)方案一的总费用为$y_{1}=0.8×50x = 40x$；当$x\leq80$时,方案二的总费用为$y_{2}=50x$；当$x ＞ 80$时,方案二的总费用为$y_{2}=50×80 + 50(x - 80)×0.6 = 30x + 1600$。
∴方案二的总费用为$y_{2}=\left\{\begin{array}{l} 50x(x\leq80),\\ 30x + 1600(x ＞ 80).\end{array}\right. $
(2)当$x ＜ 160$时，选择方案一更省钱；当$x = 160$时，选择两种购买方式花费相同；当$x ＞ 160$时，选择方案二更省钱。理由如下：①当$x\leq80$时，$\because 40x ＜ 50x$，$\therefore y_{1}＜y_{2}$，
∴选择方案一更省钱。当$80 ＜ x ＜ 160$时，$\because 40x ＜ 30x + 1600$，$\therefore y_{1}＜y_{2}$，
∴选择方案一更省钱。②当$x = 160$时，$\because 40x = 30x + 1600$，$\therefore y_{1}=y_{2}$，
∴两种购买方式花费相同。③当$x ＞ 160$时，$\because 40x ＞ 30x + 1600$，$\therefore y_{1}＞y_{2}$，
∴选择方案二更省钱。综上，当$x ＜ 160$时，选择方案一更省钱；当$x = 160$时，选择两种购买方式花费相同；当$x ＞ 160$时，选择方案二更省钱。