《2025年畅响假期衔接优化作业八年级数学华师大版》

例1 先化简,再求值：$1-(a+\frac {1}{a-1})÷\frac {a^{2}-a+1}{a^{2}-2a+1}$,其中$a= 2023^{0}+(-2)^{-1}$。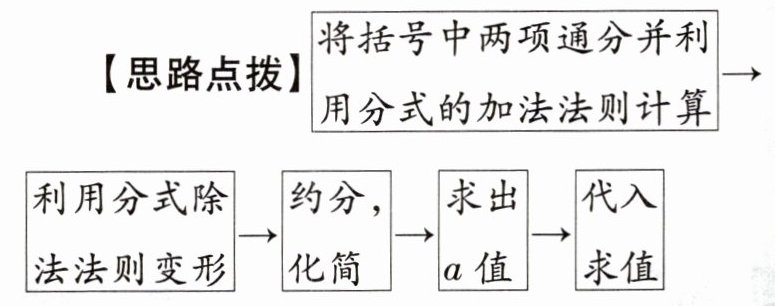

答案： 解:原式 $ = 1 - \frac{a^{2} - a + 1}{a - 1} \cdot \frac{(a - 1)^{2}}{a^{2} - a + 1} = 1 - (a - 1) = 1 - a + 1 = 2 - a $。
$ a = 2023^{0} + (-2)^{-1} = 1 - \frac{1}{2} = \frac{1}{2} $。
$ \therefore $ 当 $ a = \frac{1}{2} $ 时,原式 $ = 2 - \frac{1}{2} = \frac{3}{2} $。

变式题1 化简并求值：$(x-1-\frac {3}{x+1})÷\frac {x^{2}+4x+4}{x+1}$,其中x是方程$\frac {x-1}{2}-\frac {x-2}{5}= 0$的解。

答案： 解:原式 $ = \frac{(x + 1)(x - 1) - 3}{x + 1} ÷ \frac{(x + 2)^{2}}{x + 1} = \frac{(x + 2)(x - 2)}{x + 1} \cdot \frac{x + 1}{(x + 2)^{2}} = \frac{x - 2}{x + 2} $。
方程去分母,得 $ 5x - 5 - 2x + 4 = 0 $,解得 $ x = \frac{1}{3} $。
当 $ x = \frac{1}{3} $ 时,原式 $ = \frac{\frac{1}{3} - 2}{\frac{1}{3} + 2} = -\frac{5}{7} $。

例2 解方程：$\frac {2x+2}{x}-\frac {x+2}{x-2}= \frac {x^{2}-2}{x^{2}-2x}$。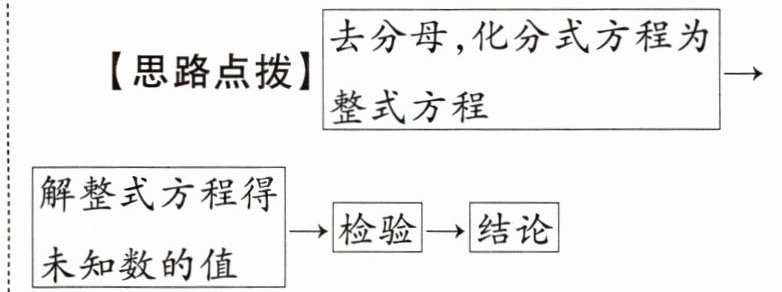

答案： 解:原方程可变形为 $ \frac{2(x + 1)}{x} - \frac{x + 2}{x - 2} = \frac{x^{2} - 2}{x(x - 2)} $,方程两边同时乘 $ x(x - 2) $,得 $ 2(x + 1)(x - 2) - x(x + 2) = x^{2} - 2 $,化简,得 $ -4x = 2 $,解得 $ x = -\frac{1}{2} $。把 $ x = -\frac{1}{2} $ 代入 $ x(x - 2) = \frac{5}{4} \neq 0 $, $ \therefore $ 原分式方程的解是 $ x = -\frac{1}{2} $。

变式题2 解分式方程$\frac {x}{3+x}-\frac {2}{2+x}= 1$时,去分母后可得到(C)
A.$x(2+x)-2(3+x)= 1$
B.$x(2+x)-2= 2+x$
C.$x(2+x)-2(3+x)= (2+x)(3+x)$
D.$x-2(3+x)= 3+x$

答案： C

例3 为缓解交通拥堵问题,小李将上班方式由自驾车改为骑电动车。他从家到达上班地点,自驾车要走的路程为10千米,骑电动车要走的路程为8千米,已知小李自驾车的速度是骑电动车速度的1.5倍,他由自驾车改为骑电动车后,时间多用了6分钟。求小李自驾车和骑电动车的速度分别是多少？
【思路点拨】分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程,注意解出分式方程后要进行检验。

答案： 解:设小李骑电动车的速度为每小时 $ x $ 千米,则自驾车的速度为每小时 $ 1.5x $ 千米。
根据题意得 $ \frac{8}{x} - \frac{10}{1.5x} = \frac{1}{10} $。解得 $ x = \frac{40}{3} $。
经检验:$ x = \frac{40}{3} $ 是原方程的解,且符合题意。
所以 $ \frac{3}{2}x = 20 $。
答:小李骑电动车的速度为每小时 $ \frac{40}{3} $ 千米,自驾车的速度为每小时 20 千米。