《2025年畅响假期衔接优化作业八年级数学华师大版》

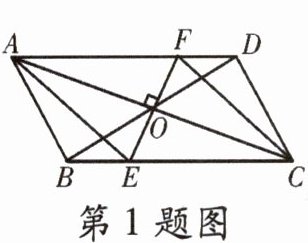
1. 如图,在$□ ABCD$中,对角线$AC与BD相交于点O$,过点$O作EF\perp AC交BC于点E$,交$AD于点F$,连结$AE$、$CF$. 则四边形$AECF$是(C)

A.梯形
B.矩形
C.菱形
D.正方形

答案： C

2. 如图,延长矩形$ABCD的边BC至点E$,使$CE= BD$,连结$AE$,若$\angle ADB= 40^{\circ}$,则$\angle E$的度数为(D)
A.$35^{\circ}$
B.$30^{\circ}$
C.$25^{\circ}$
D.$20^{\circ}$

答案： D

3. 如图,矩形纸片$ABCD$中,$AB= 6\mathrm{cm}$,$BC= 8\mathrm{cm}$,现将其沿$AE$对折,使得点$B落在边AD上的点B_{1}$处,折痕与边$BC交于点E$,则$CE$的长为(C)
A.$6\mathrm{cm}$
B.$4\mathrm{cm}$
C.$2\mathrm{cm}$
D.$1\mathrm{cm}$

答案： C

4. 如图,在菱形$ABCD$中,$M$、$N分别在AB$、$CD$上,且$AM= CN$,$MN与AC交于点O$,连结$BO$. 若$\angle DAC= 28^{\circ}$,则$\angle OBC$的度数为(C)
A.$28^{\circ}$
B.$52^{\circ}$
C.$62^{\circ}$
D.$72^{\circ}$

答案： C

5. 如图,在等腰直角$\triangle ABC$中,$AB= BC$,点$D是\triangle ABC$内部一点,$DE\perp BC$,$DF\perp AB$,垂足分别为$E$、$F$,若$CE= 3DE$,$5DF= 3AF$,$DE= 2.5$,则$AF= $(C)
A.$8$
B.$10$
C.$12.5$
D.$15$

答案： C

6. 如图,已知四边形$ABCD$为正方形,$AB= \sqrt{8}$,点$E为对角线AC$上一点,连结$DE$,过点$E作EF\perp DE$,交$BC延长线于点F$,以$DE$、$EF为邻边作矩形DEFG$,连结$CG$. 在下列结论中:①矩形$DEFG$是正方形;②$2CE+CG= \sqrt{2}AD$;③$CG平分\angle DCF$;④$CE= CF$. 其中正确的结论有(A)
A.①③
B.②④
C.①②③
D.①②③④

答案： A

7. 如图所示,线段$BC为等腰\triangle ABC$的底边,矩形$ADBE的对角线AB与DE交于点O$,若$OD= 2$,则$AC= $______4.

答案： 4

8. 如图,在边长为4的正方形$ABCD$中,$E为BC$上一点,$EF\perp AC于点F$,$EG\perp BD于点G$,那么$EF+EG= $______$\sqrt{8}$.

答案： $\sqrt{8}$

9. 如图,菱形$ABCD的顶点C在直线MN$上,若$\angle MCB= 52^{\circ}$,$\angle DCN= 18^{\circ}$,则$\angle BDC$的度数为______$35^{\circ}$.

答案： $35^{\circ}$

10. 如图,在正方形$ABCD$中,$AB= 9$,点$E在CD$边上,且$DE= 2CE$,点$P是对角线AC$上的一个动点,则$PE+PD$的最小值是$\sqrt{90}$.

答案： $\sqrt{90}$