2025年畅响假期衔接优化作业八年级数学华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年畅响假期衔接优化作业八年级数学华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
10. (11分)垫球是排球队常规训练的重要项目之一. 下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩. 测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
|测试序号|1|2|3|4|5|6|7|8|9|10|
|成绩(分)|7|6|8|7|7|5|8|7|8|7|
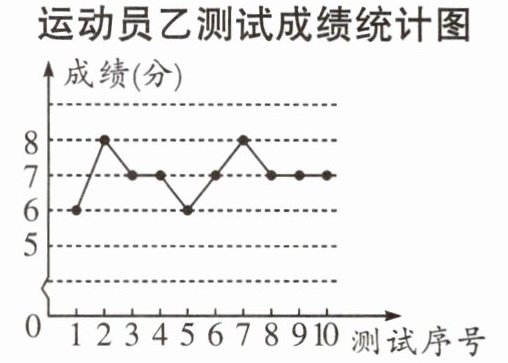
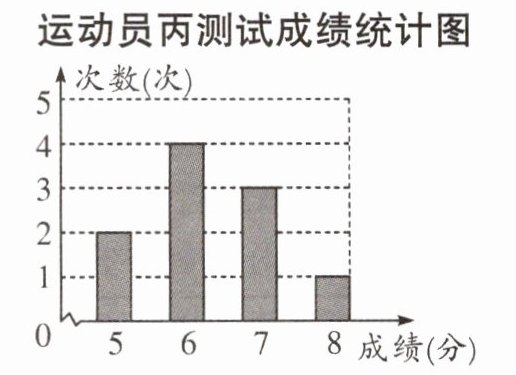
(1)求运动员甲测试成绩的众数;运动员乙测试成绩的中位数;运动员丙测试成绩的平均数.
(2)经计算三人成绩的方差分别为$s^{2}_{甲}= 0.8$、$s^{2}_{乙}= 0.4$、$s^{2}_{丙}= 0.8$,请综合分析,在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适? 为什么?
运动员甲测试成绩表
|测试序号|1|2|3|4|5|6|7|8|9|10|
|成绩(分)|7|6|8|7|7|5|8|7|8|7|


(1)求运动员甲测试成绩的众数;运动员乙测试成绩的中位数;运动员丙测试成绩的平均数.
(2)经计算三人成绩的方差分别为$s^{2}_{甲}= 0.8$、$s^{2}_{乙}= 0.4$、$s^{2}_{丙}= 0.8$,请综合分析,在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适? 为什么?
答案:
解:
(1)运动员甲测试成绩的众数和运动员乙测试成绩的中位数都是7分.
运动员丙测试成绩的平均数为$ \frac { 2 × 5 + 4 × 6 + 3 × 7 + 1 × 8 } { 2 + 4 + 3 + 1 } = 6. 3 $(分).
(2)$ \because $甲、乙、丙三人的众数分别为7;7;6;
甲、乙、丙三人的中位数分别为7;7;6;
甲、乙、丙三人的平均数分别为7;7;6.3.
$ \therefore $甲、乙较丙优秀一些.
$ \because s _ { \text { 甲 } } ^ { 2 } > s _ { \text { 乙 } } ^ { 2 } $,则乙运动员成绩更稳定,
$ \therefore $选乙运动员更合适.
(1)运动员甲测试成绩的众数和运动员乙测试成绩的中位数都是7分.
运动员丙测试成绩的平均数为$ \frac { 2 × 5 + 4 × 6 + 3 × 7 + 1 × 8 } { 2 + 4 + 3 + 1 } = 6. 3 $(分).
(2)$ \because $甲、乙、丙三人的众数分别为7;7;6;
甲、乙、丙三人的中位数分别为7;7;6;
甲、乙、丙三人的平均数分别为7;7;6.3.
$ \therefore $甲、乙较丙优秀一些.
$ \because s _ { \text { 甲 } } ^ { 2 } > s _ { \text { 乙 } } ^ { 2 } $,则乙运动员成绩更稳定,
$ \therefore $选乙运动员更合适.
11. (12分)老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数.
(2)在所抽查的学生中随机选一人谈读书感想,随后又补查另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了多少人?

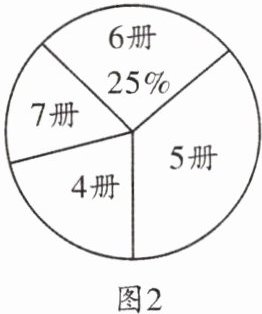
(1)求条形图中被遮盖的数,并写出册数的中位数.
(2)在所抽查的学生中随机选一人谈读书感想,随后又补查另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了多少人?


答案:
解:
(1)抽查的学生总数为$ 6 ÷ 2 5 \% = 2 4 $(人),
读书为5册的学生数为$ 2 4 - 5 - 6 - 4 = 9 $(人),
所以条形图中被遮盖的数为9,册数的中位数为5.
(2)因为4册和5册的人数和为14,中位数没改变,所以总人数不能超过27,即最多补查了3人.
(1)抽查的学生总数为$ 6 ÷ 2 5 \% = 2 4 $(人),
读书为5册的学生数为$ 2 4 - 5 - 6 - 4 = 9 $(人),
所以条形图中被遮盖的数为9,册数的中位数为5.
(2)因为4册和5册的人数和为14,中位数没改变,所以总人数不能超过27,即最多补查了3人.
查看更多完整答案,请扫码查看


