《2025年畅响假期衔接优化作业八年级数学华师大版》

11. 甲、乙两个工程队分别同时开挖两段河渠, 所挖河渠的长度$y(m)与挖掘时间x(h)$之间的关系如图所示, 根据图象信息解答下列问题:
(1) 乙队开挖到$30m$时, 用了____2$h$, 开挖$6h$时甲队比乙队多挖____10$m$.
(2) 请你求出: ①甲队在$0≤x≤6$的时段内,$y与x$之间的函数关系式; ②乙队在$2≤x≤6$的时段内,$y与x$之间的函数关系式.
(3) 在$0≤x≤6$的时段内, 当$x$为何值时, 甲、乙两队在施工过程中所挖河渠的长度相等?

(2)①设甲队在0≤x≤6的时段内y与x之间的函数关系式为y=k₁x(k₁≠0),由图象可知,函数图象过点(6,60),∴6k₁=60,解得k₁=10.∴y=10x.
②设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=k₂x + b(k₂≠0).由图象可知,函数图象过点(2,30)和(6,50).
∴$\begin{cases}2k₂ + b = 30 \\ 6k₂ + b = 50\end{cases}$，解得$\begin{cases}k₂ = 5 \\ b = 20\end{cases}$，∴y=5x+20.
(3)由题意,得10x=5x+20,解得x=4,∴当x=4h时,甲、乙两队所挖的河渠长度相等.

答案： 解:
(1)2　10
(2)①设甲队在0≤x≤6的时段内y与x之间的函数关系式为y=k_1x(k_1≠0),由图象可知,函数图象过点(6,60),
∴6k_1=60,解得k_1=10.
∴y=10x.
②设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=k_2x + b(k_2≠0).由图象可知,函数图象过点(2,30)和(6,50).
∴$\begin{cases}2k_2 + b = 30 \\ 6k_2 + b = 50\end{cases}$，解得$\begin{cases}k_2 = 5 \\ b = 20\end{cases}$，
∴y=5x+20.
(3)由题意,得10x=5x+20,解得x=4,
∴当x=4h时,甲、乙两队所挖的河渠长度相等.

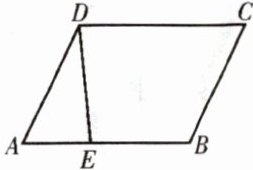
例3 如图, 已知$E是平行四边形ABCD的边AB$上的点, 连结$DE$.
(1) 在$∠ABC$的内部, 作射线$BM$, 交线段$CD于点F$, 使$∠CBF= ∠ADE$. (要求: 用尺规作图, 保留作图痕迹, 不写作法和证明)
(2) 在(1)的条件下, 求证: $\triangle ADE≌\triangle CBF$.

【名师指导】综合考查了角的作图, 平行四边形的性质和全等三角形的判定的知识, 三角形全等的判定是中考的热点, 一般以考查三角形全等的方法为主, 判定两个三角形全等, 先根据已知条件或求证的结论确定三角形, 然后再根据三角形全等的判定方法, 看缺什么条件, 再去证什么条件.

答案：

(1)解:作图如下:

(2)证明:
∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=BC.
∵∠ADE=∠CBF,
∴△ADE≌△CBF(A.S.A.).

(1) 四边形$DEBF$是矩形.
(2) 若$BE= 2$,$BF= 4$, 求$DP$的长.$\frac{5}{2}$

答案： 解:
(1)
∵DE⊥AB，BF⊥DC,
∴∠DEB=∠BFD=90°.
∵四边形ABCD是菱形，
∴AB//CD.
∴∠DEB+∠EDF=180°.
∴∠EDF=∠DEB=∠BFD=90°.
∴四边形DEBF是矩形.故答案为:矩形.
(2)如图，连结PB.
∵四边形ABCD是菱形，
∴AC垂直平分BD.
∴PB=PD.
由
(1)知，四边形DEBF是矩形，
∴DE=FB=4.设PD=BP=x，
则PE=4−x，
在Rt△PEB中，由勾股定理，得PE²+BE²=BP²，即(4−x)²+2²=x²，解得x=$\frac{5}{2}$，
∴DP=$\frac{5}{2}$.