《2025年畅响假期衔接优化作业八年级数学华师大版》

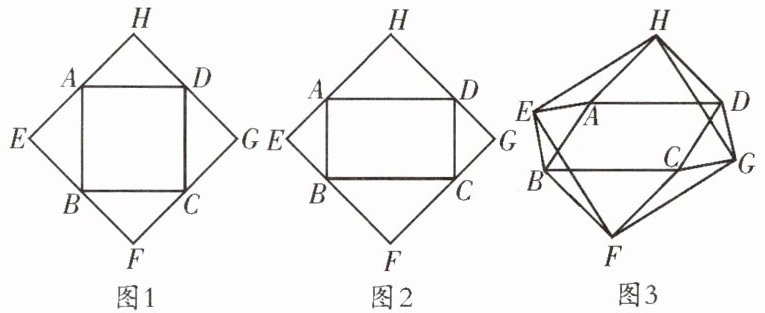
例3 以四边形$ABCD的边AB$、$BC$、$CD$、$DA$为斜边分别向外侧作等腰直角三角形,直角顶点分别为$E$、$F$、$G$、$H$,顺次连结这四个点,得四边形$EFGH$。
(1) 如图1,当四边形$ABCD$为正方形时,我们发现四边形$EFGH$是正方形；如图2,当四边形$ABCD$为矩形时,请判断：四边形$EFGH$的形状(不要求证明)。
(2) 如图3,当四边形$ABCD$为一般平行四边形时,设$\angle ADC= \alpha(0^{\circ}＜\alpha＜90^{\circ})$。
① 试用含$\alpha的代数式表示\angle HAE$；
② 求证：$HE= HG$；
③ 四边形$EFGH$是什么四边形？并说明理由。

【名师指导】①正方形具有平行四边形、矩形、菱形的所有特性,因此正方形性质的有关计算和证明题中,常常借助于菱形和矩形的性质来求解；②正方形的判定可先通过证明四边形是平行四边形,再证明其是菱形(矩形),最后证明有一个角是$90^{\circ}$(其两个邻边相等)这样的思路逐项判定。

答案：
(1)四边形EFGH是正方形
(2)①在▱ABCD中,AB//CD,
∴∠BAD=180°−∠ADC=180°−α.
∵△HAD和△EAB都是等腰直角三角形,
∴∠HAD=∠EAB=45°.
∴∠HAE=360°−∠HAD−∠EAB−∠BAD=360°−45°−45°−(180°−α)=90°+α
②证明:
∵△AEB和△DGC都是等腰直角三角形,
∴AE=$\frac{\sqrt{2}}{2}$AB,DG=$\frac{\sqrt{2}}{2}$CD.
在▱ABCD中,AB=CD,
∴AE=DG.
∵△HAD和△DGC都是等腰直角三角形，
∴HA=HD,∠HDA=∠CDG=45°.
∴∠HDG=∠HDA+∠ADC+∠CDG=90°+α=∠HAE.
∴△HAE≌△HDG(S.A.S.).
∴HE=HG.
③四边形EFGH是正方形.由②同理可得:GH=GF,FG=FE;
∵HE=HG(已证),
∴HE=GH=FG=FE.
∴四边形EFGH是菱形.
∵△HAE≌△HDG(已证),
∴∠DHG=∠AHE.又
∵∠AHD=∠AHG+∠DHG=90°,
∴∠EHG=∠AHG+∠AHE=90°.
∴四边形EFGH是正方形

拓展训练
1. 如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$BC的垂直平分线EF交BC于点D$,交$AB于点E$,且$BE= BF$,添加一个条件,仍不能证明四边形$BECF$为正方形的是(D)

A.$BC= AC$
B.$CF\perp BF$
C.$BD= DF$
D.$AC= BF$

答案： D

2. 如图,矩形$ABCD的对角线AC$、$BD交于点O$,$AB= 6$,$BC= 8$,过点$O作OE\perp AC$,交$AD于点E$,过点$E作EF\perp BD$,垂足为$F$,则$OE+EF$的值为(C)
A.$\frac{48}{5}$
B.$\frac{32}{5}$
C.$\frac{24}{5}$
D.$\frac{12}{5}$

答案： C

3. 如图,在给定的一张平行四边形纸片上作一个菱形。甲、乙两人的作法如下：
甲：连结$AC$,作$AC的垂直平分线MN分别交AD$、$AC$、$BC于点M$、$O$、$N$,连结$AN$、$CM$,则四边形$ANCM$是菱形。
乙：分别作$\angle A$、$\angle B的平分线AE$、$BF$,分别交$BC$、$AD于点E$、$F$,连结$EF$,则四边形$ABEF$是菱形。
根据两人的作法可判断(C)

A.甲正确,乙错误
B.乙正确,甲错误
C.甲、乙均正确
D.甲、乙均错误

答案： C