《2025年畅响假期衔接优化作业八年级数学华师大版》

变式题3 如图,在$\triangle ABC$的BC边的同侧分别作等边$\triangle ABD$、等边$\triangle BCF和等边\triangle ACE$。
(1)证明：四边形AEFD是平行四边形。
(2)若$AB= 3$,$AC= 4$,$BC= 5$,则$∠DFE$的度数为______$^{\circ}$。

(1)证明:∵△ABD、△BCF是等边三角形,∴AB=AD=BD,BC=CF=BF,∠CBF=∠ABD=60°.∴∠CBA=∠FBD=60°−∠ABF.
在△ABC和△DBF中，$\left\{\begin{array}{l} AB = DB,\\ ∠ABC = ∠DBF,\\ BC = BF,\end{array}\right.$
∴△ABC≌△DBF(S.A.S.).
∴DF=AC.
∵△ACE是等边三角形,∴AC=AE.
∴DF=AC=AE.同理:EF=AB=AD,
∴四边形AEFD是平行四边形
(2)150

答案：
(1)证明:
∵△ABD、△BCF是等边三角形,
∴AB=AD=BD,BC=CF=BF,∠CBF=∠ABD=60°.
∴∠CBA=∠FBD=60°−∠ABF.
　　　　　在△ABC和△DBF中，$\left\{\begin{array}{l} AB = DB,\\ ∠ABC = ∠DBF,\\ BC = BF,\end{array}\right.$
　
　
∴△ABC≌△DBF(S.A.S.).
　
　
∴DF=AC.
　
　
∵△ACE是等边三角形,
∴AC=AE.
　
　
∴DF=AC=AE.同理:EF=AB=AD,
　
　
∴四边形AEFD是平行四边形
(2)解:
∵AB=3,AC=4,BC=5,
∴BC²=AB²+AC².
　
　
∴△ABC是直角三角形,∠BAC=90°.
　
　
∵△ABD、△ACE是等边三角形,
∴∠BAD=∠CAE=60°.
　
　
∴∠DAE=360°−∠BAC−∠BAD−∠CAE=150°,
　
　
∵四边形AEFD是平行四边形,
∴∠DFE=∠DAE=150°.
　　　　　故答案为:150.

易错易混点一 不能准确理解平行四边形的性质
例1 已知点O是$□ ABCD$的对角线的交点,则下列结论：
①$AB= CD$；②$OA= OC$；③$AC= BD$；④$∠ABC= ∠ADC$；⑤$AD= CD$。其中正确的有(B)
A.2个
B.3个
C.4个
D.5个

答案： B

变式题1 如图,已知E为$□ ABCD$中DC边的延长线上一点,且$CE= DC$,连结AE,分别交BC、BD于点F、G,连结AC交BD于O,连结OF。求证：$BF= CF$。

答案： 证明:
∵四边形ABCD是平行四边形,
∴AB$\equalparallel$CD.
　
　
∴∠BAF=∠CEF,∠ABF=∠ECF;
　
　
∵CE=DC,
∴AB=CE;
　　　　　在△ABF和△ECF中,$\left\{\begin{array}{l} ∠BAF = ∠CEF,\\ AB = EC,\\ ∠ABF = ∠ECF,\end{array}\right.$
　
　
∴△ABF≌△ECF(A.S.A.).
∴BF=CF;

在$\triangle ABC$中,$∠C= 90^{\circ}$,$AC= 6$,$BC= 8$,若以A、B、C、D为顶点的四边形是平行四边形,则此平行四边形的周长为36或32或28。

答案： 36或32或28

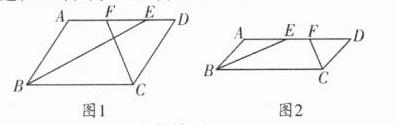
变式题2 在$□ ABCD$中,若BE平分$∠ABC$,CF平分$∠BCD$,交AD于点E、F,$BC= 9cm$,$EF= 1cm$,求AB的长。(请画出图形并求解)

答案：
解:如图1,
∵四边形ABCD是平行四边形,
　
　
∴AB=CD,AD//BC,AD=BC=9cm
　
　
∵BE平分∠ABC交AD于E,CF平分∠BCD交AD于F,
　
　
∴∠ABE=∠CBE=∠AEB,∠BCF=∠DCF=∠CFD.
　
　
∴AB=AE，DC=DF.
　
　
∵EF=1cm,
∴2AB−EF=AD.
∴2AB=9+1.
∴AB=5cm.
　　　　　如图2,
∵四边形ABCD是平行四边形，
　
　
∴AB=CD,AD//BC,AD=BC=9cm.
　
　
∵BE平分∠ABC交AD于E,CF平分∠BCD交AD于F,
　
　
∴∠ABE=∠CBE=∠AEB,∠BCF=∠DCF=∠CFD.
　
　
∴AB=AE,DC=DF.
　
　
∵EF=1cm，
∴2AB+EF=AD,
∴AB=4cm.
　　　　　综上所述，AB的长为4cm或5cm.