2025年快乐暑假天天练七年级综合河南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐暑假天天练七年级综合河南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 若关于$x的方程ax + 3x = 2的解是x= \frac{1}{4}$,则$a$的值是(
A.$-1$
B.$5$
C.$1$
D.$-5$
B
)A.$-1$
B.$5$
C.$1$
D.$-5$
答案:
【解析】:
将$x = \frac{1}{4}$代入方程$ax + 3x = 2$中,我们得到:
$a × \frac{1}{4} + 3 × \frac{1}{4} = 2$
$\frac{a}{4} + \frac{3}{4} = 2$
两边同时乘以4,得到:
$a + 3 = 8$
从上式我们可以解出:
$a = 5$
【答案】:B
将$x = \frac{1}{4}$代入方程$ax + 3x = 2$中,我们得到:
$a × \frac{1}{4} + 3 × \frac{1}{4} = 2$
$\frac{a}{4} + \frac{3}{4} = 2$
两边同时乘以4,得到:
$a + 3 = 8$
从上式我们可以解出:
$a = 5$
【答案】:B
2. 不等式组$\begin{cases}x\leqslant1,\\x>-2\end{cases} $的解集在数轴上表示正确的是(

C
)
答案:
【解析】:解不等式组$\begin{cases}x\leqslant1 \\x>-2\end{cases}$,可得其解集为$-2 < x \leqslant 1$。在数轴上表示时,$-2$处用空心圆圈(因为不包含$-2$),$1$处用实心圆点(因为包含$1$),且方向从$-2$向右到$1$。观察各选项,选项C符合要求。
【答案】:C
【答案】:C
3. 下列图形中对称轴条数最多的是(

C
)
答案:
【解析】:对称轴是指使图形沿某条直线对折后,直线两旁的部分能够完全重合的直线。
选项A:两个相交的圆组成的图形,其对称轴是两圆圆心连线所在的直线以及两圆交点连线所在的直线,共2条对称轴。
选项B:该图形由四个花瓣状图形组成,呈十字对称,水平和竖直方向各有1条对称轴,两条对角线方向也各有1条对称轴,共4条对称轴。
选项C:同心圆,任意一条经过圆心的直线都是它的对称轴,所以有无数条对称轴。
选项D:风车形状的图形,是中心对称图形,但不是轴对称图形,没有对称轴。
综上,对称轴条数最多的是选项C。
【答案】:C
选项A:两个相交的圆组成的图形,其对称轴是两圆圆心连线所在的直线以及两圆交点连线所在的直线,共2条对称轴。
选项B:该图形由四个花瓣状图形组成,呈十字对称,水平和竖直方向各有1条对称轴,两条对角线方向也各有1条对称轴,共4条对称轴。
选项C:同心圆,任意一条经过圆心的直线都是它的对称轴,所以有无数条对称轴。
选项D:风车形状的图形,是中心对称图形,但不是轴对称图形,没有对称轴。
综上,对称轴条数最多的是选项C。
【答案】:C
4. 若不等式组$\begin{cases}x>2,\\x>m\end{cases} 的解集是x>2$,则$m$的取值范围是(
A.$m\leqslant2$
B.$m\geqslant2$
C.$m\leqslant1$
D.$m>1$
A
)A.$m\leqslant2$
B.$m\geqslant2$
C.$m\leqslant1$
D.$m>1$
答案:
【解析】:
对于不等式组
$\begin{cases}x>2,\\x>m\end{cases}$
我们需要确定$m$的取值范围,使得该不等式组的解集为$x>2$。
首先,我们考虑两个不等式的交集。
第一个不等式给出$x>2$,第二个不等式给出$x>m$。
为了使不等式组的解集为$x>2$,我们需要确保$x>2$是这两个不等式的共同解集。
如果$m > 2$,那么不等式组的解集将是$x > m$,这与题目给定的解集$x>2$不符。
如果$m = 2$,那么不等式组变为
$\begin{cases}x>2,\\x>2\end{cases}$
其解集仍为$x>2$,符合题意。
如果$m < 2$,那么不等式组的解集仍然是$x>2$,因为$x>2$已经包含了$x>m$的所有解。
综上所述,我们得出$m\leqslant2$。
【答案】:A
对于不等式组
$\begin{cases}x>2,\\x>m\end{cases}$
我们需要确定$m$的取值范围,使得该不等式组的解集为$x>2$。
首先,我们考虑两个不等式的交集。
第一个不等式给出$x>2$,第二个不等式给出$x>m$。
为了使不等式组的解集为$x>2$,我们需要确保$x>2$是这两个不等式的共同解集。
如果$m > 2$,那么不等式组的解集将是$x > m$,这与题目给定的解集$x>2$不符。
如果$m = 2$,那么不等式组变为
$\begin{cases}x>2,\\x>2\end{cases}$
其解集仍为$x>2$,符合题意。
如果$m < 2$,那么不等式组的解集仍然是$x>2$,因为$x>2$已经包含了$x>m$的所有解。
综上所述,我们得出$m\leqslant2$。
【答案】:A
5. 如图,$\angle ABC和\angle ACB的外角平分线相交于点D$,如果$\angle BDC= \alpha$,那么$\angle A$等于(
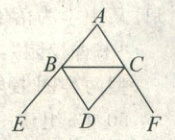
A.$90-\alpha$
B.$90-\frac{1}{2}\alpha$
C.$180-\frac{1}{2}\alpha$
D.$180-2\alpha$
D
)
A.$90-\alpha$
B.$90-\frac{1}{2}\alpha$
C.$180-\frac{1}{2}\alpha$
D.$180-2\alpha$
答案:
【解析】:在△ABC中,∠ABC和∠ACB的外角分别为∠EBC和∠FCB。因为BD、CD分别是∠EBC和∠FCB的平分线,所以∠DBC = 1/2∠EBC,∠DCB = 1/2∠FCB。
根据三角形内角和定理,∠EBC = 180° - ∠ABC,∠FCB = 180° - ∠ACB。因此:
∠DBC + ∠DCB = 1/2(∠EBC + ∠FCB) = 1/2[(180° - ∠ABC) + (180° - ∠ACB)] = 1/2[360° - (∠ABC + ∠ACB)]。
在△ABC中,∠ABC + ∠ACB = 180° - ∠A,代入上式得:
∠DBC + ∠DCB = 1/2[360° - (180° - ∠A)] = 1/2(180° + ∠A) = 90° + 1/2∠A。
在△BDC中,∠BDC = α,根据三角形内角和定理:
∠DBC + ∠DCB + ∠BDC = 180°,即90° + 1/2∠A + α = 180°。
解得:1/2∠A = 90° - α,所以∠A = 180° - 2α。
【答案】:D
根据三角形内角和定理,∠EBC = 180° - ∠ABC,∠FCB = 180° - ∠ACB。因此:
∠DBC + ∠DCB = 1/2(∠EBC + ∠FCB) = 1/2[(180° - ∠ABC) + (180° - ∠ACB)] = 1/2[360° - (∠ABC + ∠ACB)]。
在△ABC中,∠ABC + ∠ACB = 180° - ∠A,代入上式得:
∠DBC + ∠DCB = 1/2[360° - (180° - ∠A)] = 1/2(180° + ∠A) = 90° + 1/2∠A。
在△BDC中,∠BDC = α,根据三角形内角和定理:
∠DBC + ∠DCB + ∠BDC = 180°,即90° + 1/2∠A + α = 180°。
解得:1/2∠A = 90° - α,所以∠A = 180° - 2α。
【答案】:D
6. 小明从家里骑自行车到学校,每小时骑$15\mathrm{km}$,可早到$10$分钟,每小时骑$12\mathrm{km}就会迟到5$分钟。问他家到学校的路程是多少$\mathrm{km}$。设他家到学校的路程是$x\mathrm{km}$,据题意列出的方程是(
A.$\frac{x}{15}+\frac{10}{60}= \frac{x}{12}-\frac{5}{60}$
B.$\frac{x}{15}-\frac{10}{60}= \frac{x}{12}+\frac{5}{60}$
C.$\frac{x}{15}-\frac{10}{60}= \frac{x}{12}-\frac{5}{60}$
D.$\frac{x}{15}+10= \frac{x}{12}-5$
A
)A.$\frac{x}{15}+\frac{10}{60}= \frac{x}{12}-\frac{5}{60}$
B.$\frac{x}{15}-\frac{10}{60}= \frac{x}{12}+\frac{5}{60}$
C.$\frac{x}{15}-\frac{10}{60}= \frac{x}{12}-\frac{5}{60}$
D.$\frac{x}{15}+10= \frac{x}{12}-5$
答案:
【解析】:设他家到学校的路程是$x$千米,10分钟=$\frac{10}{60}$小时,5分钟=$\frac{5}{60}$小时。
当速度为每小时15千米时,所用时间为$\frac{x}{15}$小时,此时早到10分钟,那么规定时间为$\frac{x}{15}+\frac{10}{60}$小时;
当速度为每小时12千米时,所用时间为$\frac{x}{12}$小时,此时迟到5分钟,那么规定时间为$\frac{x}{12}-\frac{5}{60}$小时。
因为规定时间是固定的,所以可列方程:$\frac{x}{15}+\frac{10}{60}=\frac{x}{12}-\frac{5}{60}$。
【答案】:A
当速度为每小时15千米时,所用时间为$\frac{x}{15}$小时,此时早到10分钟,那么规定时间为$\frac{x}{15}+\frac{10}{60}$小时;
当速度为每小时12千米时,所用时间为$\frac{x}{12}$小时,此时迟到5分钟,那么规定时间为$\frac{x}{12}-\frac{5}{60}$小时。
因为规定时间是固定的,所以可列方程:$\frac{x}{15}+\frac{10}{60}=\frac{x}{12}-\frac{5}{60}$。
【答案】:A
7. 已知$x = - 3是方程(2m + 1)x - 3 = 0$的解,则$m= $
-1
。
答案:
【解析】:已知$x = - 3$是方程$(2m + 1)x - 3 = 0$的解,将$x=-3$代入方程可得:$(2m + 1)×(-3)-3 = 0$。
首先计算左边的式子:$-3(2m + 1)-3 = 0$,去括号得$-6m - 3 - 3 = 0$,合并同类项得$-6m - 6 = 0$。
然后移项可得$-6m = 6$,两边同时除以$-6$,解得$m=-1$。
【答案】:-1
首先计算左边的式子:$-3(2m + 1)-3 = 0$,去括号得$-6m - 3 - 3 = 0$,合并同类项得$-6m - 6 = 0$。
然后移项可得$-6m = 6$,两边同时除以$-6$,解得$m=-1$。
【答案】:-1
8. 将一筐橘子分给若干个小朋友,如果每人分$4$个橘子,则剩下$9$个;如果每人分$6$个橘子,则最后一个小朋友分得的橘子将少于$3$个。由以上可知共有
7
个小朋友分37
个橘子。
答案:
【解析】:设共有$x$个小朋友,则橘子的总数为$(4x + 9)$个。
当每人分$6$个橘子时,前$(x-1)$个小朋友共分得$6(x-1)$个橘子,
那么最后一个小朋友分得的橘子数为:$4x + 9 - 6(x - 1)$。
根据题意,最后一个小朋友分得的橘子少于$3$个,且大于$0$个(因为他是小朋友,至少要分到$1$个橘子,但题目中“少于$3$个”已隐含了这一点),
所以我们可以列出不等式组:
$\begin{cases}4x + 9 - 6(x - 1) < 3 \\4x + 9 - 6(x - 1) \geq 0\end{cases}$
解这个不等式组,我们得到:
从第一个不等式:$4x + 9 - 6x + 6 < 3$,
即$-2x < -12$,
得$x > 6$。
从第二个不等式:$4x + 9 - 6x + 6 \geq 0$,
即$-2x \geq -15$,
得$x \leq 7.5$。
综合两个不等式,我们得到$6 < x \leq 7.5$。
由于$x$必须是整数(因为小朋友的数量不能是小数或分数),所以$x = 7$。
将$x = 7$代入$4x + 9$,得到橘子的总数为$4 × 7 + 9 = 37$。
【答案】:$7$;$37$。
当每人分$6$个橘子时,前$(x-1)$个小朋友共分得$6(x-1)$个橘子,
那么最后一个小朋友分得的橘子数为:$4x + 9 - 6(x - 1)$。
根据题意,最后一个小朋友分得的橘子少于$3$个,且大于$0$个(因为他是小朋友,至少要分到$1$个橘子,但题目中“少于$3$个”已隐含了这一点),
所以我们可以列出不等式组:
$\begin{cases}4x + 9 - 6(x - 1) < 3 \\4x + 9 - 6(x - 1) \geq 0\end{cases}$
解这个不等式组,我们得到:
从第一个不等式:$4x + 9 - 6x + 6 < 3$,
即$-2x < -12$,
得$x > 6$。
从第二个不等式:$4x + 9 - 6x + 6 \geq 0$,
即$-2x \geq -15$,
得$x \leq 7.5$。
综合两个不等式,我们得到$6 < x \leq 7.5$。
由于$x$必须是整数(因为小朋友的数量不能是小数或分数),所以$x = 7$。
将$x = 7$代入$4x + 9$,得到橘子的总数为$4 × 7 + 9 = 37$。
【答案】:$7$;$37$。
查看更多完整答案,请扫码查看


