《2025年快乐暑假天天练七年级综合河南专版》

1. 已知$a ＜ b$,则下列各式中正确的是(D)
A.$a ＜ -b$
B.$a - 3 ＜ b - 8$
C.$a^{2} ＜ b^{2}$
D.$-3a ＞ -3b$

答案： 【解析】：对于选项A，仅知道$a ＜ b$，无法确定$a$与$-b$的大小关系，例如当$a=1$，$b=2$时，$a=-b$不成立，所以A错误；对于选项B，$a - 3 ＜ b - 8$可变形为$a - b ＜ -5$，但$a ＜ b$只能得出$a - b ＜ 0$，不能确定是否小于$-5$，例如$a=1$，$b=2$时，$1 - 3 = -2$，$2 - 8 = -6$，此时$-2 ＞ -6$，所以B错误；对于选项C，当$a=-3$，$b=1$时，$a ＜ b$，但$a^2 = 9$，$b^2 = 1$，此时$a^2 ＞ b^2$，所以C错误；对于选项D，不等式两边同时乘以一个负数，不等号方向改变，因为$a ＜ b$，两边同时乘以$-3$，可得$-3a ＞ -3b$，所以D正确。
【答案】：D

2. 如果$(x + y - 5)^{2}与|3x - 2y + 10|$互为相反数,则$x$,$y$的值为(C)
A.$x = 3$,$y = 2$
B.$x = 2$,$y = 3$
C.$x = 0$,$y = 5$
D.$x = 5$,$y = 0$

答案： 【解析】：因为一个数的平方和一个数的绝对值都是非负数，若两个非负数互为相反数，则这两个数都必须为0。所以可得方程组：
$\begin{cases}x + y - 5 = 0 \\3x - 2y + 10 = 0\end{cases}$
由第一个方程可得 $x = 5 - y$，将其代入第二个方程：
$3(5 - y) - 2y + 10 = 0$
$15 - 3y - 2y + 10 = 0$
$25 - 5y = 0$
$5y = 25$
$y = 5$
将 $y = 5$ 代入 $x = 5 - y$，得 $x = 0$。所以 $x = 0$，$y = 5$。
【答案】：C

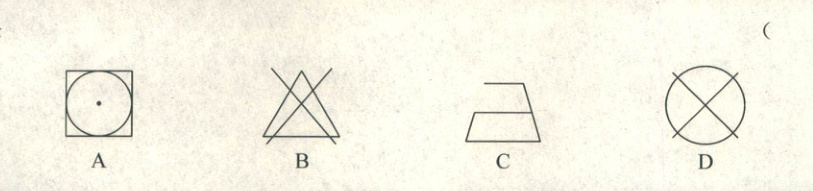
3. 在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是(C)

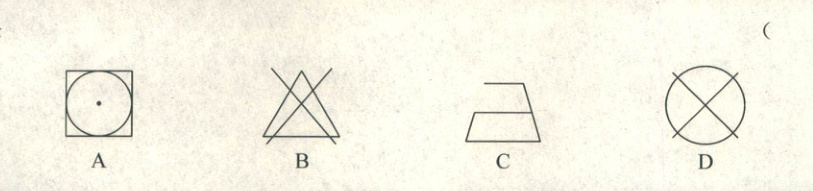
答案： 【解析】：轴对称图形是指沿一条直线折叠后，直线两旁的部分能够完全重合的图形；旋转对称图形是指绕着某一点旋转一定角度后能与自身重合的图形。
选项A：图形由正方形和内部的圆组成，正方形是轴对称图形（有4条对称轴），圆也是轴对称图形（有无数条对称轴），同时整个图形绕中心旋转90°、180°等角度后能与自身重合，运用了旋转和轴对称知识。
选项B：图形是一个由交叉线条组成的类似三角形的图案，沿中间竖直或水平直线折叠后左右或上下部分可能重合，是轴对称图形，运用了轴对称知识。
选项C：图形是一个梯形，且是一个普通的梯形（非等腰梯形），既找不到一条直线使其折叠后完全重合（不是轴对称图形），绕任意一点旋转一定角度后也不能与自身重合（不是旋转对称图形），没有运用旋转或轴对称知识。
选项D：图形是一个圆内有两条交叉的直径，圆是轴对称图形（直径所在直线都是对称轴），两条交叉直径将圆分成的部分绕圆心旋转90°、180°等角度后能重合，运用了旋转和轴对称知识。
【答案】：C

4. 某商店进了一批商品,每件商品的进价为$a$元,若要获利$20\%$,则每件商品的零售价为(D)
A.$20\%a$
B.$(1 - 20\%)a$
C.$\frac{a}{1 + 20\%}$
D.$(1 + 20\%)a$

答案： 【解析】：设每件商品的零售价为$x$元。
根据题意，商店希望获得$20\%$的利润，即利润为$20\% × a = 0.2a$元。
因此，零售价$x$应等于进价$a$加上利润，即$x = a + 0.2a$。
合并同类项，得$x = (1 + 0.2)a = 1.2a$。
也可以表示为$x = (1 + 20\%)a$。
【答案】：D

5. 如图,$\triangle ABC≌\triangle DEF$,则此图中相等的线段有(D)

A.1对
B.2对
C.3对
D.4对

答案： 【解析】：因为△ABC≌△DEF，根据全等三角形的性质，全等三角形的对应边相等。所以AB=DE，AC=DF，BC=EF。
由图可知，BC=BE+EC，EF=EC+CF，因为BC=EF，所以BE+EC=EC+CF，等式两边同时减去EC，可得BE=CF。
综上，相等的线段有AB=DE，AC=DF，BC=EF，BE=CF，共4对。
【答案】：D

6. 在方程$2x + 5y = 1$中,用含$x的代数式表示y$为$y = \frac{1 - 2x}{5}$。

答案： 【解析】：
首先，我们有方程 $2x + 5y = 1$。
为了用含$x$的代数式表示$y$，我们需要解出$y$。
将方程 $2x + 5y = 1$ 改写为 $5y = 1 - 2x$。
接着，两边同时除以5，得到 $y = \frac{1 - 2x}{5}$。
【答案】：$y = \frac{1 - 2x}{5}$。

7. 当$0 ＜ a ＜ b ＜ 1$时,用“$＞$”或“$＜$”填空：
①$\frac{1}{a}$＞$\frac{1}{b}$,②$a^{2}$＜$b^{2}$。

答案： 【解析】：
① 对于$\frac{1}{a}$和$\frac{1}{b}$，由于$0 ＜ a ＜ b ＜ 1$，当分母增大时（且保持为正数），分数会减小。因此，$\frac{1}{a} ＞ \frac{1}{b}$。
② 对于$a^{2}$和$b^{2}$，由于$0 ＜ a ＜ b ＜ 1$，且$a$和$b$都是正数，当底数增大时，其平方也会增大。因此，$a^{2} ＜ b^{2}$。
【答案】：
① $＞$
② $＜$

8. 如图,将等边三角形$ABC$剪去一个角后,则$\angle 1 + \angle 2$等于240°

答案： 【解析】：因为等边三角形$ABC$的每个内角都是$60^{\circ}$，所以$\angle A = \angle B=\angle C = 60^{\circ}$。将三角形剪去一个角后，得到一个四边形，$\angle 1$和$\angle 2$是这个四边形的两个内角。根据四边形的内角和为$360^{\circ}$，可知这个四边形的四个内角之和为$360^{\circ}$，其中另外两个内角分别是原等边三角形的$\angle B$和$\angle C$，即$60^{\circ}$和$60^{\circ}$。所以$\angle 1+\angle 2=360^{\circ}-\angle B - \angle C=360^{\circ}-60^{\circ}-60^{\circ}=240^{\circ}$。
【答案】：240°