《2025年快乐暑假天天练七年级综合河南专版》

10.解下列方程组,

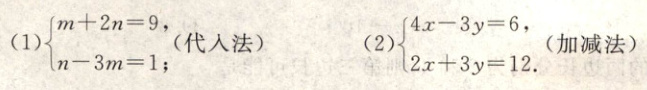
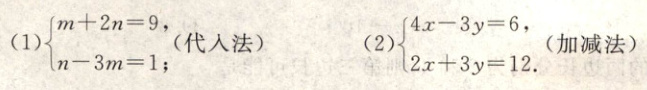
答案： 1. （1）用代入法解方程组$\begin{cases}m + 2n=9\\n−3m = 1\end{cases}$：
由方程$n−3m = 1$，可得$n=3m + 1$。
将$n = 3m+1$代入方程$m + 2n=9$中，得到：
$m+2(3m + 1)=9$。
去括号：$m + 6m+2 = 9$。
移项：$m+6m=9 - 2$。
合并同类项：$7m=7$。
系数化为$1$：$m = 1$。
把$m = 1$代入$n=3m + 1$，得$n=3×1 + 1=4$。
所以方程组的解为$\begin{cases}m = 1\\n = 4\end{cases}$。
2. （2）用加减法解方程组$\begin{cases}4x−3y = 6\\2x+3y = 12\end{cases}$：
解：将两个方程相加，$(4x−3y)+(2x + 3y)=6 + 12$。
去括号：$4x−3y+2x + 3y=6 + 12$。
合并同类项：$(4x+2x)+(-3y + 3y)=18$，即$6x=18$。
系数化为$1$：$x = 3$。
把$x = 3$代入$2x+3y = 12$中，得$2×3+3y = 12$。
即$6+3y = 12$。
移项：$3y=12 - 6$。
合并同类项：$3y=6$。
系数化为$1$：$y = 2$。
所以方程组的解为$\begin{cases}x = 3\\y = 2\end{cases}$。
综上，（1）$\begin{cases}m = 1\\n = 4\end{cases}$；（2）$\begin{cases}x = 3\\y = 2\end{cases}$。

11.根据国家发改委实施“阶梯电价”的有美文件要求,某市结合地方实际,决定从2014年4月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表;

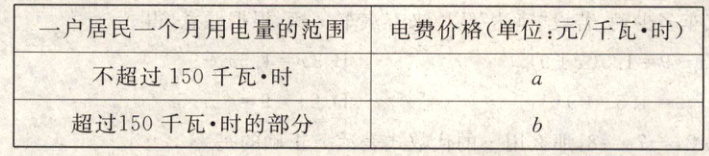
2014年5月份,该市甲户居民用电100千瓦.时,交电费60元;乙户居民用电200 千瓦.时,交电费122.5元
(1)上表中,a= ______0.6b=0.65;
(2)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦.时时,其当月的平均电价每千瓦.时不超过0,62元？250千瓦时

答案： 【解析】：
(1)首先，我们根据甲户居民的用电情况来求解a的值。
由题意知，甲户居民用电100千瓦时，交电费60元，因此我们可以得到方程：
$100a = 60$
解这个方程，我们得到：
$a = \frac{60}{100} = 0.6$
接着，我们利用乙户居民的用电情况来求解b的值。
乙户居民用电200千瓦时，交电费122.5元。根据阶梯电价收费标准，我们可以得到方程：
$150 × 0.6 + (200 - 150)b = 122.5$
解这个方程，我们得到：
$90 + 50b = 122.5$
$50b = 32.5$
$b = \frac{32.5}{50} = 0.65$
(2)接下来，我们需要找出满足当月平均电价每千瓦时不超过0.62元的用电量范围。
设该市一户居民用电$x$千瓦时，其当月的平均电价每千瓦时为$y$元。
当$0 \leq x \leq 150$时，由$y \leq 0.62$，我们可以得到：
$0.6 \leq 0.62$
这个不等式恒成立，所以在这个电量范围内，平均电价都不会超过0.62元。
当$x ＞ 150$时，我们需要解不等式：
$0.62 \geq \frac{150 × 0.6 + (x - 150) × 0.65}{x}$
化简后得到：
$0.62x \geq 90 + 0.65x - 97.5$
$0.03x \leq 7.5$
$x \leq 250$
综合以上两种情况，我们可以得出当居民月用电量不超过250千瓦时时，其当月的平均电价每千瓦时不超过0.62元。
【答案】：
(1)$a = 0.6$，$b = 0.65$
(2)月用电量不超过250千瓦时