2025年快乐暑假天天练七年级综合河南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐暑假天天练七年级综合河南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 已知 $ x = 2 $ 是关于 $ x $ 的方程 $ 3x + a = 0 $ 的一个解,则 $ a $ 的值是 (
A.-6
B.-3
C.-4
D.-5
A
)A.-6
B.-3
C.-4
D.-5
答案:
【解析】:
题目给出的方程是 $3x + a = 0$,并且已知 $x = 2$ 是该方程的一个解。将 $x = 2$ 代入方程中,可以得到:
$3 \cdot 2 + a = 0$
$6 + a = 0$
解这个方程,得到:
$a = -6$
【答案】:A
题目给出的方程是 $3x + a = 0$,并且已知 $x = 2$ 是该方程的一个解。将 $x = 2$ 代入方程中,可以得到:
$3 \cdot 2 + a = 0$
$6 + a = 0$
解这个方程,得到:
$a = -6$
【答案】:A
2. 下列平面图形中,不能镶嵌平面的图形是 (
A.任意一种三角形
B.任意一种四边形
C.任意一种正五边形
D.任意一种正六边形
C
)A.任意一种三角形
B.任意一种四边形
C.任意一种正五边形
D.任意一种正六边形
答案:
【解析】:
对于选项A,任意一种三角形,其内角和为$180^\circ$。由于$360^\circ ÷ 180^\circ = 2$,即两个三角形就可以在一个顶点处完成镶嵌,所以三角形能够镶嵌平面。
对于选项B,任意一种四边形,其内角和为$360^\circ$。因此,一个四边形就可以在一个顶点处完成镶嵌,所以四边形也能够镶嵌平面。
对于选项C,任意一种正五边形,其内角为$108^\circ$(由公式$(n-2) × 180^\circ ÷ n$计算得出,其中n=5)。由于$360^\circ ÷ 108^\circ$有余数,即正五边形不能在一个顶点处与其他正五边形完全吻合,所以正五边形不能镶嵌平面。
对于选项D,任意一种正六边形,其内角为$120^\circ$(由公式$(n-2) × 180^\circ ÷ n$计算得出,其中n=6)。由于$360^\circ ÷ 120^\circ = 3$,即三个正六边形就可以在一个顶点处完成镶嵌,所以正六边形能够镶嵌平面。
综上所述,不能镶嵌平面的图形是任意一种正五边形。
【答案】:C
对于选项A,任意一种三角形,其内角和为$180^\circ$。由于$360^\circ ÷ 180^\circ = 2$,即两个三角形就可以在一个顶点处完成镶嵌,所以三角形能够镶嵌平面。
对于选项B,任意一种四边形,其内角和为$360^\circ$。因此,一个四边形就可以在一个顶点处完成镶嵌,所以四边形也能够镶嵌平面。
对于选项C,任意一种正五边形,其内角为$108^\circ$(由公式$(n-2) × 180^\circ ÷ n$计算得出,其中n=5)。由于$360^\circ ÷ 108^\circ$有余数,即正五边形不能在一个顶点处与其他正五边形完全吻合,所以正五边形不能镶嵌平面。
对于选项D,任意一种正六边形,其内角为$120^\circ$(由公式$(n-2) × 180^\circ ÷ n$计算得出,其中n=6)。由于$360^\circ ÷ 120^\circ = 3$,即三个正六边形就可以在一个顶点处完成镶嵌,所以正六边形能够镶嵌平面。
综上所述,不能镶嵌平面的图形是任意一种正五边形。
【答案】:C
3. 如图, $ \triangle ABC $ 与 $ \triangle DEF $ 关于直线 $ MN $ 轴对称,则以下结论中错误的是 (
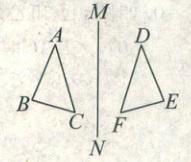
A.$ AB // DF $
B.$ \angle B = \angle E $
C.$ AB = DE $
D.$ AD $ 的连线被 $ MN $ 垂直平分
A
)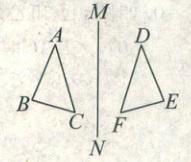
A.$ AB // DF $
B.$ \angle B = \angle E $
C.$ AB = DE $
D.$ AD $ 的连线被 $ MN $ 垂直平分
答案:
【解析】:因为△ABC与△DEF关于直线MN轴对称,根据轴对称的性质可知:
对应角相等,所以∠B=∠E,选项B正确;
对应边相等,所以AB=DE(AB的对应边是DE,而非DF),选项C正确;
对应点的连线被对称轴垂直平分,点A与点D是对应点,所以AD的连线被MN垂直平分,选项D正确;
由图可知AB与DF不平行,选项A错误。
【答案】:A
对应角相等,所以∠B=∠E,选项B正确;
对应边相等,所以AB=DE(AB的对应边是DE,而非DF),选项C正确;
对应点的连线被对称轴垂直平分,点A与点D是对应点,所以AD的连线被MN垂直平分,选项D正确;
由图可知AB与DF不平行,选项A错误。
【答案】:A
4. 足球比赛的记分规则:胜一场得 3 分,平一场得 1 分,负一场得 0 分.某队打了 14 场,负 5 场,共得 19 分,那么这个队胜了 (
A.3 场
B.4 场
C.5 场
D.6 场
5
)A.3 场
B.4 场
C.5 场
D.6 场
答案:
【解析】:设这个队胜了$x$场,平了$y$场。
根据题意,该队共打了$14$场,负了$5$场,所以胜和平的场数之和为$14 - 5 = 9$场,即$x + y = 9$。
再根据记分规则,胜一场得$3$分,平一场得$1$分,负一场得$0$分,该队共得$19$分,所以$3x + y = 19$。
现在我们有一个方程组:
$\begin{cases}x + y = 9 \\3x + y = 19\end{cases}$
解这个方程组,我们可以得到:
从第一个方程中解出$y = 9 - x$,
代入第二个方程得:$3x + (9 - x) = 19$,
解得:$x = 5$,
将$x = 5$代入第一个方程得:$y = 4$。
所以,这个队胜了$5$场。
【答案】:C
根据题意,该队共打了$14$场,负了$5$场,所以胜和平的场数之和为$14 - 5 = 9$场,即$x + y = 9$。
再根据记分规则,胜一场得$3$分,平一场得$1$分,负一场得$0$分,该队共得$19$分,所以$3x + y = 19$。
现在我们有一个方程组:
$\begin{cases}x + y = 9 \\3x + y = 19\end{cases}$
解这个方程组,我们可以得到:
从第一个方程中解出$y = 9 - x$,
代入第二个方程得:$3x + (9 - x) = 19$,
解得:$x = 5$,
将$x = 5$代入第一个方程得:$y = 4$。
所以,这个队胜了$5$场。
【答案】:C
5. 已知 $ \begin{cases} 3a + 4b = 8, \\ a + 6b = 4, \end{cases} $ 则 $ a - b $ 等于 (
A.2
B.$ \frac{8}{3} $
C.3
D.1
A
)A.2
B.$ \frac{8}{3} $
C.3
D.1
答案:
【解析】:
已知方程组为:
$\begin{cases}3a + 4b = 8, \quad (1) \\a + 6b = 4. \quad (2)\end{cases}$
为了求解$a - b$,我们可以将方程
(1)减去方程
(2),即:
$(3a + 4b) - (a + 6b) = 8 - 4$,
化简得:
$2a - 2b = 4$,
进一步化简,得到:
$a - b = 2$。
【答案】:A
已知方程组为:
$\begin{cases}3a + 4b = 8, \quad (1) \\a + 6b = 4. \quad (2)\end{cases}$
为了求解$a - b$,我们可以将方程
(1)减去方程
(2),即:
$(3a + 4b) - (a + 6b) = 8 - 4$,
化简得:
$2a - 2b = 4$,
进一步化简,得到:
$a - b = 2$。
【答案】:A
6. 某班有 40 名同学去看演出,购买甲、乙两种票共用去 370 元,其中甲种票每张 10 元,乙种票每张 8 元,设购买了甲种票 $ x $ 张,乙种票 $ y $ 张,由此可列出方程组:
$\begin{cases} x + y = 40 \\ 10x + 8y = 370 \end{cases}$
.
答案:
【解析】:根据题目所提供的信息,我们知道班级总共有40名同学去看演出,这意味着购买的甲种票和乙种票的总数应该是40张。设购买了甲种票$x$张,乙种票$y$张,所以第一种等量关系可以表示为甲种票的张数加上乙种票的张数等于总人数,即$x + y = 40$。
另外,题目中还提到购买甲、乙两种票共用去370元,甲种票每张10元,乙种票每张8元。那么购买甲种票花费的钱数就是$10x$元,购买乙种票花费的钱数就是$8y$元,它们的总和是370元,所以第二种等量关系可以表示为甲种票的总花费加上乙种票的总花费等于总钱数,即$10x + 8y = 370$。
综上所述,可列出的方程组为:
$\begin{cases}x + y = 40 \\10x + 8y = 370\end{cases}$
【答案】:$\begin{cases} x + y = 40 \\ 10x + 8y = 370 \end{cases}$
另外,题目中还提到购买甲、乙两种票共用去370元,甲种票每张10元,乙种票每张8元。那么购买甲种票花费的钱数就是$10x$元,购买乙种票花费的钱数就是$8y$元,它们的总和是370元,所以第二种等量关系可以表示为甲种票的总花费加上乙种票的总花费等于总钱数,即$10x + 8y = 370$。
综上所述,可列出的方程组为:
$\begin{cases}x + y = 40 \\10x + 8y = 370\end{cases}$
【答案】:$\begin{cases} x + y = 40 \\ 10x + 8y = 370 \end{cases}$
7. 三元一次方程组 $ \begin{cases} x - y = 1, \\ y - z = 1, \\ x + z = 4 \end{cases} $ 的解是
$\begin{cases}x = 3 \\y = 2 \\z = 1\end{cases}$
.
答案:
【解析】:
首先,我们有方程组:
$\begin{cases}x - y = 1 \quad (1) \\y - z = 1 \quad (2) \\x + z = 4 \quad (3)\end{cases}$,
从方程
(1)和方程
(2)中,我们可以将两个方程相加,得到:
$x - z = 2 \quad (4)$,
接下来,我们将方程
(3)与方程
(4)相加,得到:
$2x = 6$,
从中我们可以解出:
$x = 3$,
将 $x = 3$ 代入方程
(1),我们得到:
$3 - y = 1$,
从中解出:
$y = 2$,
再将 $x = 3$ 代入方程
(3),我们得到:
$3 + z = 4$,
从中解出:
$z = 1$,
综上所述,方程组的解为:
$\begin{cases}x = 3 \\y = 2 \\z = 1\end{cases}$。
【答案】:$\begin{cases}x = 3 \\y = 2 \\z = 1\end{cases}$。
首先,我们有方程组:
$\begin{cases}x - y = 1 \quad (1) \\y - z = 1 \quad (2) \\x + z = 4 \quad (3)\end{cases}$,
从方程
(1)和方程
(2)中,我们可以将两个方程相加,得到:
$x - z = 2 \quad (4)$,
接下来,我们将方程
(3)与方程
(4)相加,得到:
$2x = 6$,
从中我们可以解出:
$x = 3$,
将 $x = 3$ 代入方程
(1),我们得到:
$3 - y = 1$,
从中解出:
$y = 2$,
再将 $x = 3$ 代入方程
(3),我们得到:
$3 + z = 4$,
从中解出:
$z = 1$,
综上所述,方程组的解为:
$\begin{cases}x = 3 \\y = 2 \\z = 1\end{cases}$。
【答案】:$\begin{cases}x = 3 \\y = 2 \\z = 1\end{cases}$。
8. 如图,点 $ P $ 是 $ \angle AOB $ 内部的一定点.
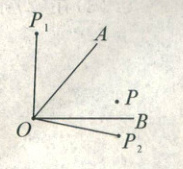
(1) 若 $ \angle AOB = 50^{\circ} $,作点 $ P $ 关于 $ OA $ 的对称点 $ P_1 $,作点 $ P $ 关于 $ OB $ 的对称点 $ P_2 $,连结 $ OP_1 $、$ OP_2 $,则 $ \angle P_1OP_2 = $
(2) 若 $ \angle AOB = \alpha $,点 $ C $、$ D $ 分别在射线 $ OA $、$ OB $ 上移动,当 $ \triangle PCD $ 的周长最小时,则 $ \angle CPD = $

(1) 若 $ \angle AOB = 50^{\circ} $,作点 $ P $ 关于 $ OA $ 的对称点 $ P_1 $,作点 $ P $ 关于 $ OB $ 的对称点 $ P_2 $,连结 $ OP_1 $、$ OP_2 $,则 $ \angle P_1OP_2 = $
100
度;(2) 若 $ \angle AOB = \alpha $,点 $ C $、$ D $ 分别在射线 $ OA $、$ OB $ 上移动,当 $ \triangle PCD $ 的周长最小时,则 $ \angle CPD = $
$ 180 - 2\alpha $
度(用含 $ \alpha $ 的代数式表示).
答案:
【解析】:
(1) 因为点 $ P $ 关于 $ OA $ 的对称点是 $ P_1 $,所以 $ OA $ 垂直平分 $ PP_1 $,则 $ OP_1 = OP $,且 $ \angle AOP_1 = \angle AOP $。同理,点 $ P $ 关于 $ OB $ 的对称点是 $ P_2 $,所以 $ OB $ 垂直平分 $ PP_2 $,则 $ OP_2 = OP $,且 $ \angle BOP_2 = \angle BOP $。已知 $ \angle AOB = 50^\circ $,即 $ \angle AOP + \angle BOP = 50^\circ $,所以 $ \angle P_1OP_2 = \angle AOP_1 + \angle AOP + \angle BOP + \angle BOP_2 = 2(\angle AOP + \angle BOP) = 2 × 50^\circ = 100^\circ $。
(2) 分别作点 $ P $ 关于 $ OA $、$ OB $ 的对称点 $ P_1 $、$ P_2 $,连接 $ P_1P_2 $,分别交 $ OA $、$ OB $ 于点 $ C $、$ D $,此时 $ \triangle PCD $ 的周长最小,等于 $ P_1P_2 $ 的长。由对称性质可知,$ PC = P_1C $,$ PD = P_2D $,$ \angle P_1OA = \angle POA $,$ \angle P_2OB = \angle POB $,所以 $ \angle P_1OP_2 = 2\angle AOB = 2\alpha $。在 $ \triangle P_1OP_2 $ 中,$ \angle P_1 + \angle P_2 = 180^\circ - \angle P_1OP_2 = 180^\circ - 2\alpha $。因为 $ \angle P_1 = \angle CPO $,$ \angle P_2 = \angle DPO $,所以 $ \angle CPD = 180^\circ - (\angle CPO + \angle DPO) = 180^\circ - (\angle P_1 + \angle P_2) = 180^\circ - (180^\circ - 2\alpha) = 2\alpha $?不对,这里需要重新计算。
实际上,$ \angle CPO = \angle P_1 $,$ \angle DPO = \angle P_2 $,所以 $ \angle CPD = 180^\circ - (\angle CPO + \angle DPO) = 180^\circ - (\angle P_1 + \angle P_2) $。而 $ \angle P_1 + \angle P_2 = 180^\circ - \angle P_1OP_2 = 180^\circ - 2\alpha $,所以 $ \angle CPD = 180^\circ - (180^\circ - 2\alpha) = 2\alpha $?不对,应该是 $ \angle CPD = 180^\circ - (\angle PCD + \angle PDC) $,而 $ \angle PCD = \angle P_1 + \angle P_1OC $,$ \angle PDC = \angle P_2 + \angle P_2OD $,这里更简便的是利用四边形内角和或三角形内角和。
因为 $ P_1C = PC $,所以 $ \angle P_1 = \angle CPP_1 $,同理 $ \angle P_2 = \angle DPP_2 $。在 $ \triangle P_1PP_2 $ 中,$ \angle P_1PP_2 + \angle P_1 + \angle P_2 = 180^\circ $,而 $ \angle P_1PP_2 = 180^\circ - \angle CPD $,所以 $ 180^\circ - \angle CPD + \angle P_1 + \angle P_2 = 180^\circ $,即 $ \angle CPD = \angle P_1 + \angle P_2 $。又因为 $ \angle P_1 + \angle P_2 = 180^\circ - \angle P_1OP_2 = 180^\circ - 2\alpha $,所以 $ \angle CPD = 180^\circ - 2\alpha $。
【答案】:
(1) 100;
(2) $ 180 - 2\alpha $
(1) 因为点 $ P $ 关于 $ OA $ 的对称点是 $ P_1 $,所以 $ OA $ 垂直平分 $ PP_1 $,则 $ OP_1 = OP $,且 $ \angle AOP_1 = \angle AOP $。同理,点 $ P $ 关于 $ OB $ 的对称点是 $ P_2 $,所以 $ OB $ 垂直平分 $ PP_2 $,则 $ OP_2 = OP $,且 $ \angle BOP_2 = \angle BOP $。已知 $ \angle AOB = 50^\circ $,即 $ \angle AOP + \angle BOP = 50^\circ $,所以 $ \angle P_1OP_2 = \angle AOP_1 + \angle AOP + \angle BOP + \angle BOP_2 = 2(\angle AOP + \angle BOP) = 2 × 50^\circ = 100^\circ $。
(2) 分别作点 $ P $ 关于 $ OA $、$ OB $ 的对称点 $ P_1 $、$ P_2 $,连接 $ P_1P_2 $,分别交 $ OA $、$ OB $ 于点 $ C $、$ D $,此时 $ \triangle PCD $ 的周长最小,等于 $ P_1P_2 $ 的长。由对称性质可知,$ PC = P_1C $,$ PD = P_2D $,$ \angle P_1OA = \angle POA $,$ \angle P_2OB = \angle POB $,所以 $ \angle P_1OP_2 = 2\angle AOB = 2\alpha $。在 $ \triangle P_1OP_2 $ 中,$ \angle P_1 + \angle P_2 = 180^\circ - \angle P_1OP_2 = 180^\circ - 2\alpha $。因为 $ \angle P_1 = \angle CPO $,$ \angle P_2 = \angle DPO $,所以 $ \angle CPD = 180^\circ - (\angle CPO + \angle DPO) = 180^\circ - (\angle P_1 + \angle P_2) = 180^\circ - (180^\circ - 2\alpha) = 2\alpha $?不对,这里需要重新计算。
实际上,$ \angle CPO = \angle P_1 $,$ \angle DPO = \angle P_2 $,所以 $ \angle CPD = 180^\circ - (\angle CPO + \angle DPO) = 180^\circ - (\angle P_1 + \angle P_2) $。而 $ \angle P_1 + \angle P_2 = 180^\circ - \angle P_1OP_2 = 180^\circ - 2\alpha $,所以 $ \angle CPD = 180^\circ - (180^\circ - 2\alpha) = 2\alpha $?不对,应该是 $ \angle CPD = 180^\circ - (\angle PCD + \angle PDC) $,而 $ \angle PCD = \angle P_1 + \angle P_1OC $,$ \angle PDC = \angle P_2 + \angle P_2OD $,这里更简便的是利用四边形内角和或三角形内角和。
因为 $ P_1C = PC $,所以 $ \angle P_1 = \angle CPP_1 $,同理 $ \angle P_2 = \angle DPP_2 $。在 $ \triangle P_1PP_2 $ 中,$ \angle P_1PP_2 + \angle P_1 + \angle P_2 = 180^\circ $,而 $ \angle P_1PP_2 = 180^\circ - \angle CPD $,所以 $ 180^\circ - \angle CPD + \angle P_1 + \angle P_2 = 180^\circ $,即 $ \angle CPD = \angle P_1 + \angle P_2 $。又因为 $ \angle P_1 + \angle P_2 = 180^\circ - \angle P_1OP_2 = 180^\circ - 2\alpha $,所以 $ \angle CPD = 180^\circ - 2\alpha $。
【答案】:
(1) 100;
(2) $ 180 - 2\alpha $
查看更多完整答案,请扫码查看


