《2025年快乐暑假天天练七年级综合河南专版》

9. 解不等式组$\begin{cases}x - 2＜0,①\\5x + 1＞2(x - 1).②\end{cases} $

答案： 【解析】：
对于不等式①：$x - 2 \lt 0$，
移项可得：$x \lt 2$。
对于不等式②：$5x + 1 \gt 2(x - 1)$，
去括号：$5x + 1 \gt 2x - 2$，
移项：$5x - 2x \gt -2 - 1$，
合并同类项：$3x \gt -3$，
系数化为1：$x \gt -1$。
综合不等式①和不等式②的解，取交集，得到不等式组的解集为：$-1 \lt x \lt 2$。
【答案】：$-1 \lt x \lt 2$。

10. 已知等腰三角形的底边长为5cm,一腰上的中线把原三角形的周长分为两部分,其差为3cm,求该等腰三角形的腰长。

答案： 【解析】：
设等腰三角形的腰长为 $x$ cm。
根据题意，一腰上的中线把原三角形的周长分为两部分，这两部分的差为3cm。
所以有两种情况：
1. 上半部分的周长为 $x + \frac{x}{2}$，下半部分的周长为 $\frac{x}{2} + 5$。
根据题意，有 $x + \frac{x}{2} - (\frac{x}{2} + 5) = 3$，
化简得 $x - 5 = 3$，
解得 $x = 8$。
2. 上半部分的周长为 $x + \frac{x}{2}$，下半部分的周长为 $\frac{x}{2} + 5$。
根据题意，有 $\frac{x}{2} + 5 - (x + \frac{x}{2}) = 3$，
化简得 $5 - x = 3$，
解得 $x = 2$。
接下来，需要验证这两个解是否都符合题意。
对于 $x = 8$，等腰三角形的三边长为8cm, 8cm, 5cm，满足三角形的三边关系，即任意两边之和大于第三边，所以这是一个合理的解。
对于 $x = 2$，等腰三角形的三边长为2cm, 2cm, 5cm，不满足三角形的三边关系，因为 $2 + 2 ＜ 5$，所以这不是一个合理的解。
综上所述，该等腰三角形的腰长为8cm。
【答案】：8cm

11. 阅读下面材料：
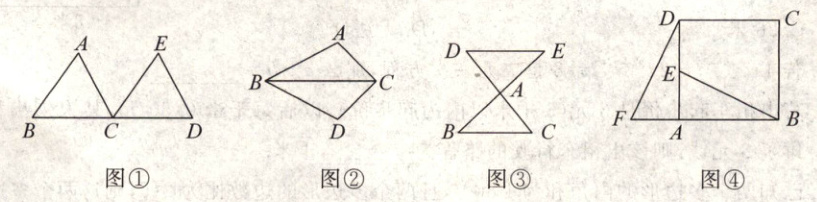
如图①,把$\triangle ABC沿直线BC平行移动线段BC$的长度,可以变到$\triangle ECD$的位置；如图②,以$BC$为轴,把$\triangle ABC翻折180^{\circ}$,可以变到$\triangle DBC$的位置；如图③,以点$A$为中心,把$\triangle ABC旋转180^{\circ}$,可以变到$\triangle AED$的位置。
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方式得到的。这种只改变位置,不改变形状、大小的图形变换,叫做三角形的全等变换。
回答下列问题：
(1) 在图④中,可以通过平行移动、翻折、旋转中的哪一种方式怎样变化,使$\triangle ABE变到\triangle ADF$的位置；
(2) 指出图中线段$BE与DF$之间的关系,并说明理由。

答案： 【解析】：
(1) 观察图④，四边形ABCD是矩形（根据矩形性质，对边平行且相等，四个角为直角）。点A为旋转中心，AB与AD是矩形的邻边，∠BAD=90°。△ABE要变到△ADF的位置，AB旋转到AD的位置，AE旋转到AF的位置，因为AB⊥AD，AE⊥AF（矩形中相关垂直关系可推出），所以旋转角为90°。
(2) 由
(1)知△ABE绕点A逆时针旋转90°得到△ADF，根据全等变换的性质，旋转不改变图形的形状和大小，所以△ABE≌△ADF。因此，对应边BE=DF，对应角∠ABE=∠ADF。在矩形ABCD中，∠ADF+∠FDC=90°，又因为∠ABE=∠ADF，所以∠ABE+∠FDC=90°。延长BE交DF于点G，在△DGB中，∠DGB=180°-(∠ABE+∠FDC)=180°-90°=90°，所以BE⊥DF。综上，BE与DF的关系是BE=DF且BE⊥DF。
【答案】：
(1) 以点A为中心，逆时针旋转90°；
(2) BE=DF且BE⊥DF