2025年快乐暑假天天练七年级综合河南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐暑假天天练七年级综合河南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 若$a>b$,则下列不等式中,不成立的是(
A.$a+5>b+5$
B.$a-5>b-5$
C.$5a>5b$
D.$-5a>-5b$
D
)A.$a+5>b+5$
B.$a-5>b-5$
C.$5a>5b$
D.$-5a>-5b$
答案:
【解析】:
根据不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变。
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变。
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变。
A. 根据性质
(1),在不等式$a > b$两边同时加5,得到$a + 5 > b + 5$,所以A选项是正确的。
B. 同样根据性质
(1),在不等式$a > b$两边同时减5,得到$a - 5 > b - 5$,所以B选项是正确的。
C. 根据性质
(2),在不等式$a > b$两边同时乘以5,得到$5a > 5b$,所以C选项是正确的。
D. 根据性质
(3),在不等式$a > b$两边同时乘以-5,应得到$-5a < -5b$,与D选项中的$-5a > -5b$相矛盾,所以D选项是错误的。
【答案】:D
根据不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变。
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变。
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变。
A. 根据性质
(1),在不等式$a > b$两边同时加5,得到$a + 5 > b + 5$,所以A选项是正确的。
B. 同样根据性质
(1),在不等式$a > b$两边同时减5,得到$a - 5 > b - 5$,所以B选项是正确的。
C. 根据性质
(2),在不等式$a > b$两边同时乘以5,得到$5a > 5b$,所以C选项是正确的。
D. 根据性质
(3),在不等式$a > b$两边同时乘以-5,应得到$-5a < -5b$,与D选项中的$-5a > -5b$相矛盾,所以D选项是错误的。
【答案】:D
2. 商店出售下列形状的地砖:①长方形;②正方形;③正五边形;④正六边形.若只选购其中某一种地砖镶嵌地面,可供选择的地砖共有(
A.1种
B.2种
C.3种
D.4种
C
)A.1种
B.2种
C.3种
D.4种
答案:
【解析】:
对于长方形地砖:其内角为$90^\circ$ ,围绕一点拼$360^\circ$ ,需要$\frac{360^\circ}{90^\circ}=4$个,可以镶嵌平面。
对于正方形地砖:其内角为$90^\circ$ ,围绕一点拼$360^\circ$ ,需要$\frac{360^\circ}{90^\circ}=4$个,可以镶嵌平面。
对于正五边形地砖:其内角为$108^\circ$ ,$360^\circ÷108^\circ=\frac{10}{3}$ ,结果不是整数,不能镶嵌平面。
对于正六边形地砖:其内角为$120^\circ$ ,围绕一点拼$360^\circ$ ,需要$\frac{360^\circ}{120^\circ}=3$个,可以镶嵌平面。
所以可供选择的地砖有长方形、正方形、正六边形,共$3$种。
【答案】:C
对于长方形地砖:其内角为$90^\circ$ ,围绕一点拼$360^\circ$ ,需要$\frac{360^\circ}{90^\circ}=4$个,可以镶嵌平面。
对于正方形地砖:其内角为$90^\circ$ ,围绕一点拼$360^\circ$ ,需要$\frac{360^\circ}{90^\circ}=4$个,可以镶嵌平面。
对于正五边形地砖:其内角为$108^\circ$ ,$360^\circ÷108^\circ=\frac{10}{3}$ ,结果不是整数,不能镶嵌平面。
对于正六边形地砖:其内角为$120^\circ$ ,围绕一点拼$360^\circ$ ,需要$\frac{360^\circ}{120^\circ}=3$个,可以镶嵌平面。
所以可供选择的地砖有长方形、正方形、正六边形,共$3$种。
【答案】:C
3. 若当$x= 3$时,代数式$3x^{2}-5ax+10$的值为7,则$a$的值是(
A.2
B.-2
C.1
D.-1
2
)A.2
B.-2
C.1
D.-1
答案:
【解析】:当$x = 3$时,代数式$3x^2 - 5ax + 10$的值为$7$,将$x = 3$代入代数式可得:
$\begin{aligned}3×3^2 - 5a×3 + 10&=7\\3×9 - 15a + 10&=7\\27 - 15a + 10&=7\\37 - 15a&=7\\-15a&=7 - 37\\-15a&=-30\\a&=2\end{aligned}$
【答案】:A
$\begin{aligned}3×3^2 - 5a×3 + 10&=7\\3×9 - 15a + 10&=7\\27 - 15a + 10&=7\\37 - 15a&=7\\-15a&=7 - 37\\-15a&=-30\\a&=2\end{aligned}$
【答案】:A
4. 为了搞活经济,某商场将一种商品$A$按标价9折出售,仍获利润10%,若商品$A$标价为33元,那么商品进货价为(
A.31元
B.30.2元
C.29.7元
D.27元
D
)A.31元
B.30.2元
C.29.7元
D.27元
答案:
【解析】:设商品的进货价为$x$元。
根据题意,商品按标价的$9$折出售,即售价为$33 × 0.9$元,仍能获得$10\%$的利润。
因此,售价等于进货价加上$10\%$的进货价,即$1.1x$元。
根据以上关系,我们可以列出方程:
$33 × 0.9 = 1.1x$,
解这个方程,我们得到:
$x = \frac{33 × 0.9}{1.1} = 27$,
【答案】:D
根据题意,商品按标价的$9$折出售,即售价为$33 × 0.9$元,仍能获得$10\%$的利润。
因此,售价等于进货价加上$10\%$的进货价,即$1.1x$元。
根据以上关系,我们可以列出方程:
$33 × 0.9 = 1.1x$,
解这个方程,我们得到:
$x = \frac{33 × 0.9}{1.1} = 27$,
【答案】:D
5. 已知$\left\{\begin{array}{l} x= 2,\\ y= 1\end{array} \right. 是二元一次方程组\left\{\begin{array}{l} mx+ny= 8,\\ nx-my= 1\end{array} \right. $的解,则$2m-n$的值为(
A.16
B.4
C.2
D.1
B
)A.16
B.4
C.2
D.1
答案:
【解析】:
已知$x=2$,$y=1$是方程组的解,将其代入方程组得:
$\begin{cases}2m + n = 8,\\2n - m = 1.\end{cases}$
由$2m + n = 8$可得$n = 8 - 2m$,将其代入$2n - m = 1$中,得:
$2(8 - 2m) - m = 1$,
展开括号得$16 - 4m - m = 1$,
合并同类项得$16 - 5m = 1$,
移项得$-5m = 1 - 16$,
即$-5m = -15$,
两边同时除以$-5$得$m = 3$。
将$m = 3$代入$n = 8 - 2m$,得$n = 8 - 2×3 = 2$。
所以$2m - n = 2×3 - 2 = 4$。
【答案】:B
已知$x=2$,$y=1$是方程组的解,将其代入方程组得:
$\begin{cases}2m + n = 8,\\2n - m = 1.\end{cases}$
由$2m + n = 8$可得$n = 8 - 2m$,将其代入$2n - m = 1$中,得:
$2(8 - 2m) - m = 1$,
展开括号得$16 - 4m - m = 1$,
合并同类项得$16 - 5m = 1$,
移项得$-5m = 1 - 16$,
即$-5m = -15$,
两边同时除以$-5$得$m = 3$。
将$m = 3$代入$n = 8 - 2m$,得$n = 8 - 2×3 = 2$。
所以$2m - n = 2×3 - 2 = 4$。
【答案】:B
6. 如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为$a$、$b(a>b)$,则$a-b$等于(
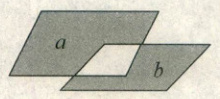
A.3
B.4
C.5
D.6
6
)
A.3
B.4
C.5
D.6
答案:
【解析】:
设重叠部分的面积为$c$。
根据题意,两个平行四边形的面积分别为18和12。
第一个平行四边形的面积可以表示为$a+c$,即$a+c=18$。
第二个平行四边形的面积可以表示为$b+c$,即$b+c=12$。
要求$a-b$,可以通过两个等式相减得到:
$(a+c)-(b+c)=18-12$,
$a-b=6$。
【答案】:D
设重叠部分的面积为$c$。
根据题意,两个平行四边形的面积分别为18和12。
第一个平行四边形的面积可以表示为$a+c$,即$a+c=18$。
第二个平行四边形的面积可以表示为$b+c$,即$b+c=12$。
要求$a-b$,可以通过两个等式相减得到:
$(a+c)-(b+c)=18-12$,
$a-b=6$。
【答案】:D
7. 小玉买书用48元钱,付款时恰好用了1元和5元的纸币共12张.那么1元的纸币用了
3
张.
答案:
【解析】:设1元的纸币用了$x$张,那么5元的纸币用了$12 - x$张。
根据题意,1元纸币的总金额加上5元纸币的总金额等于48元,即:
$1 × x + 5 × (12 - x) = 48$
展开得:
$x + 60 - 5x = 48$
合并同类项:
$-4x = -12$
解得:
$x = 3$
所以,1元的纸币用了3张。
【答案】:3
根据题意,1元纸币的总金额加上5元纸币的总金额等于48元,即:
$1 × x + 5 × (12 - x) = 48$
展开得:
$x + 60 - 5x = 48$
合并同类项:
$-4x = -12$
解得:
$x = 3$
所以,1元的纸币用了3张。
【答案】:3
8. 如图,在$\triangle ABC$中,$∠C= 70^{\circ }$,沿图中虚线截去$∠C$,则$∠1+∠2= $
$250^{\circ}$
.
答案:
【解析】:
$\because\angle 1$,$\angle 2$是$\triangle ABC$的外角,
$\therefore \angle 1=\angle C+\angle CBA$,$\angle 2=\angle C+\angle CAB$,
$\therefore \angle 1+\angle 2=\angle C+\angle CBA+\angle CAB+\angle C$,
$\because \angle CBA+\angle C+\angle CAB=180^{\circ}$,$\angle C=70^{\circ}$,
$\therefore \angle 1+\angle 2=180^{\circ}+70^{\circ}=250^{\circ}$。
【答案】:
$250^{\circ}$
$\because\angle 1$,$\angle 2$是$\triangle ABC$的外角,
$\therefore \angle 1=\angle C+\angle CBA$,$\angle 2=\angle C+\angle CAB$,
$\therefore \angle 1+\angle 2=\angle C+\angle CBA+\angle CAB+\angle C$,
$\because \angle CBA+\angle C+\angle CAB=180^{\circ}$,$\angle C=70^{\circ}$,
$\therefore \angle 1+\angle 2=180^{\circ}+70^{\circ}=250^{\circ}$。
【答案】:
$250^{\circ}$
9. 现规定一种新的运算,$\begin{vmatrix} a&b\\ c&d\end{vmatrix} = ad-bc$,那么$\begin{vmatrix} 3&3\\ 2-x&4\end{vmatrix} = 9$时,$x= $
1
.
答案:
【解析】:根据新运算规则,$\begin{vmatrix} 3&3\\ 2 - x&4\end{vmatrix}=3×4 - 3×(2 - x)$。已知该式等于$9$,则可列出方程:
$\begin{aligned}3×4 - 3×(2 - x)&=9\\12 - 6 + 3x&=9\\6 + 3x&=9\\3x&=9 - 6\\3x&=3\\x&=1\end{aligned}$
【答案】:1
$\begin{aligned}3×4 - 3×(2 - x)&=9\\12 - 6 + 3x&=9\\6 + 3x&=9\\3x&=9 - 6\\3x&=3\\x&=1\end{aligned}$
【答案】:1
查看更多完整答案,请扫码查看


