《2025年实验班提优训练四年级数学上册人教版》

1. 学校开展安全疏散演练,要求学生选择最短路线尽快到达操场内的长方形安全区域(如下图)。如果明明站在点 A 的位置,静静站在点 B 的位置,那么请在下图中分别画出他们到达安全区域的最短路线。

答案：

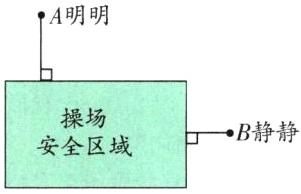
[提示]因为从直线外一点到这条直线所画的值直线段最短,所以只要过点A和点B分别向操场安全区域最近的值画垂直线段即可。

2. 如下图,小兔想先去拔胡萝卜,再去河边钓鱼。你能帮小兔设计一条最近的路线吗?

答案：

[提示]因为两点之间,线段最短,所以小兔要去胡萝卜地只要以两点为端点,画一条线段即可。由直线外一点到这条直线所画的垂直线段最短可知,从胡萝卜地向河边画垂直线段即可。

3. 下图是李明扔垒球的落地点,如果你是裁判员,那么该怎样测量他的成绩?请在图中画出待测量的线段。

如果图中线段1厘米代表10米,那么李明扔垒球的成绩是多少米?

答案：

待测量线段长2厘米。 2×10=20(米) 【提示】测量他的成绩时应该从垒球落地点向起掷线画垂直线段,量出线段的长度,因为图中1厘米代表10米,所以求李明的成绩,就用线段的长度乘10。

4. 有两个上底、下底和腰分别为 4 厘米、8 厘米和 6 厘米的等腰梯形。现在要把它们拼成一个平行四边形,这个平行四边形的周长是多少厘米?

答案： 8+4+6+6=24(厘米)
24×2-6-6=36(厘米)
[提示]等腰梯形的特征是两腰相等,先求出等腰梯形的周长。再拼一拼,发现把两个相同的等腰梯形拼成一个平行四边形,腰重合,从两个等腰梯形的周长和中减去两条腰长,即可求出平行四边形的周长。

5. 一个直角梯形的高是 20 厘米,其中一条腰长 25 厘米。如果上底增加15 厘米,那么就成为一个正方形。求原来梯形的周长。

答案：
20×3-15+25=70(厘米)
[提示]根据题意,可以先画图再分析(如下图),通过分析图形可以发现,求原来梯形的周长,可以用正方形三条边的长度之和减去上底增加的15厘米,再加上腰长25厘米。