《2025年实验班提优训练四年级数学上册人教版》

1. 数一数,下面的图形中一共有多少条线段？

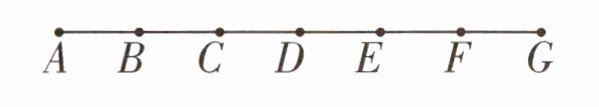
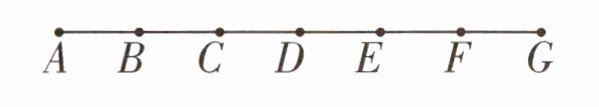
答案： 6+5+4+3+2+1=21(条)
【提示】找出基本线段有6条，由两条基本线段组成的线段有5条，由三条基本线段组成的线段有4条，由四条基本线段组成的线段有3条，由五条基本线段组成的线段有2条，由六条基本线段组成的线段有1条，一共有6+5+4+3+2+1=21(条)线段。

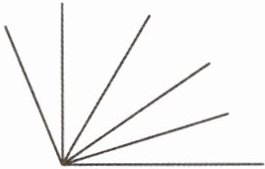
2. 下图中一共有(15)个角。

答案： 15 【提示】先数单个的，再数组合的，共有5+4+3+2+1=15(个)角。

3. 数一数,下图中一共有(20)个三角形。

答案： 20 【提示】(4+3+2+1)×2=20(个)

4. 下面的图形中共有多少个角？

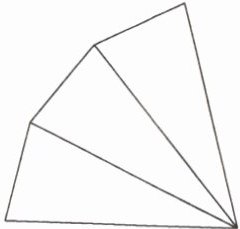
答案： 14个 【提示】单个的角有9个，由2个角组合而成的角有4个，由3个角组合而成的角有1个，一共有9+4+1=14(个)角。

5. 求出下图中∠1和∠2的度数。

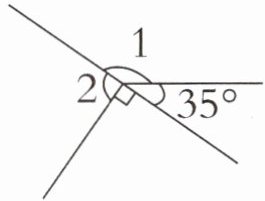
答案： ∠1=145° ∠2=90° 【提示】由图可知，∠1+35°为平角，则∠1=180°-35°=145°。∠2+90°为平角，则∠2=180°-90°=90°。

6. 如右下图,求∠1的度数。(三角形三个内角的和为180°)

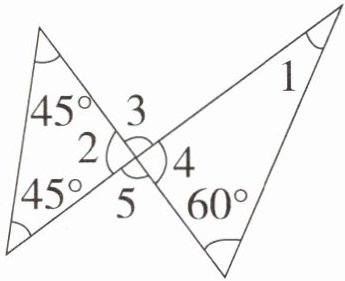
答案： ∠2=180°-45°-45°=90°，因为∠2+∠3=∠3+∠4=180°，所以∠2=∠4=90°，∠1=180°-90°-60°=30°。
【提示】由“∠2和∠3组成一个平角，∠3和∠4也组成一个平角，得出∠2=∠4”是解决此题的关键。

7. 如右下图,若∠2= ∠3,则∠4等于多少度？∠5呢？

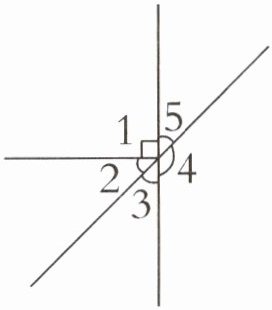
答案： ∠4=135° ∠5=45°
【提示】由图可知，∠1+∠2+∠3=180°，且∠1=90°，∠2=∠3，所以∠3=(180°-90°)÷2=45°。∠4=180°-∠3=180°-45°=135°。又因为∠3+∠4=∠4+∠5=180°，所以∠5=∠3=45°