《2025年实验班提优训练四年级数学上册人教版》

1. 小马虎做一道乘法计算题时,把其中一个因数23误写成26,结果得到的积比正确的积多363。正确的积是多少？下面是小明的想法：
|另一个因数用▲表示,正确的算式是▲×23,表示23个▲,错误的算式是(▲×26),表示(26个▲),这样就比正确的积多(3)个▲,也就是363,所以……|

你同意小明的想法吗？请你根据小明的想法写出算式并解答。
同意 363÷(26 - 23)=121
121×23=2783

答案： ▲×26 26个▲ 3
同意 363÷(26 - 23)=121
121×23=2783
[提示]把23写成26，多写了3，结果比正确的积多363，用363÷3求出另一个因数，进而求出正确的积｡

2. 东东和乐乐计算同一道三位数乘两位数的算式,列竖式时东东把两位数个位上的6抄成了9,结果比乐乐的正确答案多了561。已知这个两位数十位上的数字比个位上的数字多3,则这道算式的正确结果是多少？

答案： 561÷(9 - 6)=187
6 + =9
187×96=17952
[提示]根据题意可知,在用两位数个位上的数字去乘三位数时,个位上本应为6,却被抄成了9,积多了561,所以这个三位数是561÷(9 - )=187;再根据“这个两位数十位上的数字比个位上数字多3可知,这个两位数是96,所以这道算式足7×96=795｡

(1)$\begin{array}{r} □□5\\ ×\quad4□\\ \hline 3□□\\ □2□□\quad\\ \hline 1□□05\end{array} $
30105125
(2)$\begin{array}{r} □76\\ ×\quad□□\\ \hline 18□0\\ □□□□\quad\\ \hline 31□□0\end{array} $
3858300680

答案：
(1)05×41=12505 [提示]根据第一个因数的个位上,积的个位上也是5,可知第二个因数的个位上可能是1、3、57、9｡因为第一次乘得的积是三位数,且积最高位上知第二个因数个位上只能是1或3若第二个因数的个位上是3,则第一个因数百位上就是这与第二次乘得的积是四位数不符,所以第二个因数的个位上只能是1,第一个因数的百位上是3｡再从第二次乘得的积的末位数字分析,4与5相乘末位数字因为积的十位上是0,所以第一次乘得积十位上也是0,据此可以得出这个乘法算式是305×41｡
(2)376×85=31 0 [提示]由于积的个位上是0,因此第二个因数的个位上是5｡由此,我们可以得到第一个因数与5相乘得1880,第一个因数的百位上是3｡最后,376×□5=31 0,所以第二个因数的十位上是8(9太大,7太小)｡

4. 如果$A\neq B$,且A、B满足下面的算式,那么$A+B$等于多少？

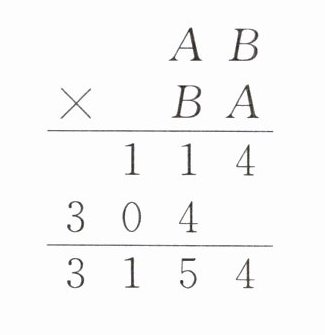
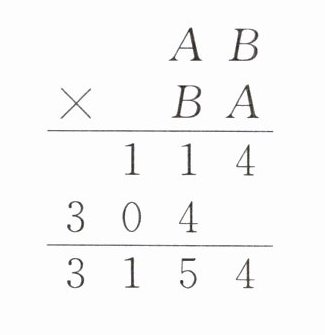
答案： A + B=11 [提示]由AB×A=114,AB×B=304可知“B×B”的积的末位是4,“A×B”的积的末位也是4,B可取2或8,对应的A可取2、7或3、8｡因为A≠B,所以对应组合应为A是7、B是2或A是3、B是8｡因为38×83=3154,所以A为3,B为8,A + B=3 + 8=11｡