第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1 算一算。(π取3.14)
$2^{2}\pi =$
$3^{2}\pi =$
$4^{2}\pi =$
$5^{2}\pi =$
$6^{2}\pi =$
$2^{2}\pi =$
12.56
$3^{2}\pi =$
28.26
$4^{2}\pi =$
50.24
$5^{2}\pi =$
78.5
$6^{2}\pi =$
113.04
答案:
12.56 28.26 50.24 78.5 113.04
(1)利用方格估计下图中圆的面积。

(2)如图,把一个半径为r的圆平均分成若干份后,拼成一个近似的平行四边形。

①拼成的平行四边形的底相当于圆周长的
②拼成的平行四边形与原来的圆相比,面积
③根据平行四边形的面积公式可以推导出圆的面积公式是$S=$
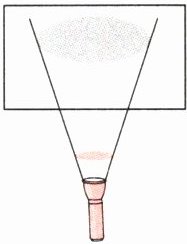
(3)老师带领同学们进行“影子的形成”科学小实验,林林发现把圆形纸片放在手电筒前的某一位置时,形成的圆形影子的半径是圆形纸片半径的3倍。此时,圆形影子的周长是圆形纸片的

12 52 (估计结果合理即可)
(2)如图,把一个半径为r的圆平均分成若干份后,拼成一个近似的平行四边形。

①拼成的平行四边形的底相当于圆周长的
一半
,用字母表示是πr
;高相当于圆的半径
,用字母表示是r
。②拼成的平行四边形与原来的圆相比,面积
不变
,周长变大
。(填“变大”“变小”或“不变”)③根据平行四边形的面积公式可以推导出圆的面积公式是$S=$
πr²
。(3)老师带领同学们进行“影子的形成”科学小实验,林林发现把圆形纸片放在手电筒前的某一位置时,形成的圆形影子的半径是圆形纸片半径的3倍。此时,圆形影子的周长是圆形纸片的
3
倍,圆形影子的面积是圆形纸片的9
倍。
答案:
(1)12 52 (估计结果合理即可)
(2)①一半 πr 半径 r
②不变 变大 ③πr²
(3)3 9
(1)12 52 (估计结果合理即可)
(2)①一半 πr 半径 r
②不变 变大 ③πr²
(3)3 9
3 求下面各图形的面积。


答案:
3.14×4²=50.24(dm²)
3.14×(6÷2)²=28.26(cm²)
3.14×(12÷2)²÷2=56.52(m²)
3.14×(6÷2)²=28.26(cm²)
3.14×(12÷2)²÷2=56.52(m²)
4 如图,把圆平均分成若干份,可以拼成一个近似的长方形,长方形的长是3.14 cm,则圆的面积是多少平方厘米?


答案:
3.14×2÷3.14÷2=1(cm)
3.14×1²=3.14(cm²)
答:圆的面积是3.14 cm²。
3.14×1²=3.14(cm²)
答:圆的面积是3.14 cm²。
查看更多完整答案,请扫码查看


