《2025年初中必刷题七年级数学上册人教版》

变式练3 观察下面一列数:$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6}……那么第9$个数是$-\frac{1}{9}$,第$2022$个数是$\frac{1}{2022}$.

答案： 【解析】：
观察数列$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6}\ldots$可以发现，数列的每一项的绝对值都是其位置的倒数，即第$n$项的绝对值为$\frac{1}{n}$。同时，数列的符号交替出现，即奇数项为负，偶数项为正。
对于第9个数，由于9是奇数，所以其符号为负。其绝对值为$\frac{1}{9}$，因此第9个数是$-\frac{1}{9}$。
对于第2022个数，由于2022是偶数，所以其符号为正。其绝对值为$\frac{1}{2022}$，因此第2022个数是$\frac{1}{2022}$。
【答案】：
第9个数是$-\frac{1}{9}$；
第2022个数是$\frac{1}{2022}$。

$1. \underline{①正整数}、$$\underline{②零}、$$\underline{③负整数}$统称为整数；$\underline{④正分数}$和$\underline{⑤负分数}$统称为分数；整数可以写成$\underline{⑥分母为1的分数}$的形式；可以写成$\underline{⑦分数}$形式的数称为有理数。

答案： 解：①正整数；②零；③负整数；④正分数；⑤负分数；⑥分母为1的分数；⑦分数。

2. 有理数的分类
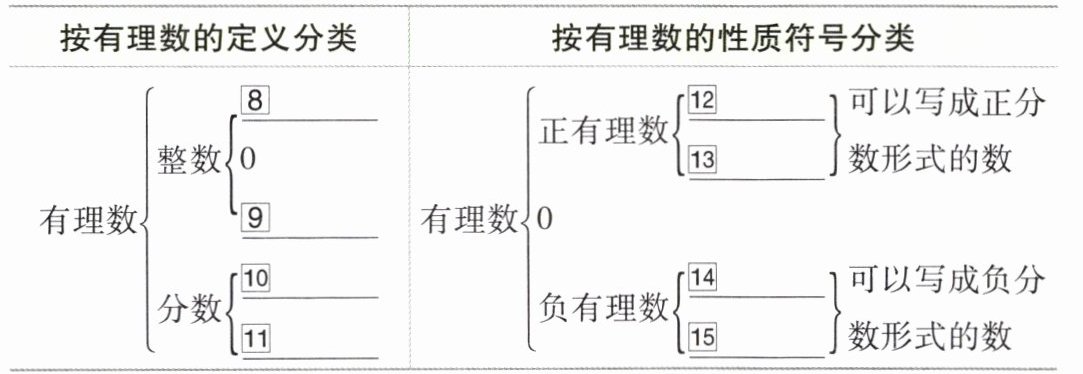
|按有理数的定义分类|按有理数的性质符号分类|
|----|----|
|有理数$\begin{cases}整数\begin{cases}\underline{⑧正整数}\\0\\\underline{⑨负整数}\end{cases}\\分数\begin{cases}\underline{⑩正分数}\\\underline{⑪负分数}\end{cases}\end{cases}$|有理数$\begin{cases}正有理数\begin{cases}\underline{⑫正整数}\\ \underline{⑬正分数}\end{cases}&可以写成正分数形式的数\\0\\负有理数\begin{cases}\underline{⑭负整数}\\ \underline{⑮负分数}\end{cases}&可以写成负分数形式的数\end{cases}$|

答案： 【解析】：
题目考查有理数的分类。
按定义分类：
整数包含正整数、零、负整数。
分数包含正分数、负分数。
按性质符号分类：
正有理数包含正整数、正分数。
负有理数包含负整数、负分数。
根据以上知识填空即可。
【答案】：
⑧正整数；
⑨负整数；
⑩正分数；
⑪负分数；
⑫正整数；
⑬正分数；
⑭负整数；
⑮负分数。