13. 已知$2x + y = 4$,求$[(x - y)^{2}-(x + y)^{2}+y(2x - y)]÷(-2y)$的值。
答案:
【解析】:
本题可先化简$[(x - y)^{2}-(x + y)^{2}+y(2x - y)]\div(-2y)$,再将$2x + y = 4$整体代入化简后的式子求值。
- **步骤一:化简$[(x - y)^{2}-(x + y)^{2}+y(2x - y)]\div(-2y)$。**
**利用完全平方公式$(a\pm b)^2=a^2\pm 2ab + b^2$分别展开$(x - y)^{2}$与$(x + y)^{2}$:**
$(x - y)^{2}=x^{2}-2xy + y^{2}$,$(x + y)^{2}=x^{2}+2xy + y^{2}$。
**计算$(x - y)^{2}-(x + y)^{2}$:**
将上述展开式代入可得:
$(x - y)^{2}-(x + y)^{2}=(x^{2}-2xy + y^{2})-(x^{2}+2xy + y^{2})$
去括号:$x^{2}-2xy + y^{2}-x^{2}-2xy - y^{2}$
合并同类项:$(x^{2}-x^{2})+(-2xy - 2xy)+(y^{2}-y^{2})=-4xy$。
**计算$y(2x - y)$:**
根据单项式乘多项式的运算法则,用单项式去乘多项式的每一项,再把所得的积相加,可得:
$y(2x - y)=2xy - y^{2}$。
**计算$(x - y)^{2}-(x + y)^{2}+y(2x - y)$:**
将前面计算的结果代入可得:
$(x - y)^{2}-(x + y)^{2}+y(2x - y)=-4xy + 2xy - y^{2}=-2xy - y^{2}$。
**计算$[(x - y)^{2}-(x + y)^{2}+y(2x - y)]\div(-2y)$:**
将$-2xy - y^{2}$代入可得:
$(-2xy - y^{2})\div(-2y)$
根据多项式除以单项式的运算法则,先把这个多项式的每一项分别除以这个单项式,再把所得的商相加,可得:
$(-2xy - y^{2})\div(-2y)=(-2xy)\div(-2y)+(-y^{2})\div(-2y)=x+\frac{1}{2}y$。
- **步骤二:将$2x + y = 4$变形后代入化简后的式子求值。**
对$2x + y = 4$两边同时除以$2$,可得$x+\frac{1}{2}y = 2$。
因为化简后的式子$x+\frac{1}{2}y$的值就是原式的值,所以原式的值为$2$。
【答案】:$2$
本题可先化简$[(x - y)^{2}-(x + y)^{2}+y(2x - y)]\div(-2y)$,再将$2x + y = 4$整体代入化简后的式子求值。
- **步骤一:化简$[(x - y)^{2}-(x + y)^{2}+y(2x - y)]\div(-2y)$。**
**利用完全平方公式$(a\pm b)^2=a^2\pm 2ab + b^2$分别展开$(x - y)^{2}$与$(x + y)^{2}$:**
$(x - y)^{2}=x^{2}-2xy + y^{2}$,$(x + y)^{2}=x^{2}+2xy + y^{2}$。
**计算$(x - y)^{2}-(x + y)^{2}$:**
将上述展开式代入可得:
$(x - y)^{2}-(x + y)^{2}=(x^{2}-2xy + y^{2})-(x^{2}+2xy + y^{2})$
去括号:$x^{2}-2xy + y^{2}-x^{2}-2xy - y^{2}$
合并同类项:$(x^{2}-x^{2})+(-2xy - 2xy)+(y^{2}-y^{2})=-4xy$。
**计算$y(2x - y)$:**
根据单项式乘多项式的运算法则,用单项式去乘多项式的每一项,再把所得的积相加,可得:
$y(2x - y)=2xy - y^{2}$。
**计算$(x - y)^{2}-(x + y)^{2}+y(2x - y)$:**
将前面计算的结果代入可得:
$(x - y)^{2}-(x + y)^{2}+y(2x - y)=-4xy + 2xy - y^{2}=-2xy - y^{2}$。
**计算$[(x - y)^{2}-(x + y)^{2}+y(2x - y)]\div(-2y)$:**
将$-2xy - y^{2}$代入可得:
$(-2xy - y^{2})\div(-2y)$
根据多项式除以单项式的运算法则,先把这个多项式的每一项分别除以这个单项式,再把所得的商相加,可得:
$(-2xy - y^{2})\div(-2y)=(-2xy)\div(-2y)+(-y^{2})\div(-2y)=x+\frac{1}{2}y$。
- **步骤二:将$2x + y = 4$变形后代入化简后的式子求值。**
对$2x + y = 4$两边同时除以$2$,可得$x+\frac{1}{2}y = 2$。
因为化简后的式子$x+\frac{1}{2}y$的值就是原式的值,所以原式的值为$2$。
【答案】:$2$
1. 计算$a^{3}\cdot (a^{3})^{2}$的结果是()
A. $a^{8}$
B. $a^{9}$
C. $a^{11}$
D. $a^{18}$
A. $a^{8}$
B. $a^{9}$
C. $a^{11}$
D. $a^{18}$
答案:
B
2. 下列计算正确的是()
A. $a^{6}+a^{6}=2a^{12}$
B. $2^{-2}÷2^{0}×2^{3}=32$
C. $(-\frac{1}{2}ab^{2})\cdot (-2a^{2}b)^{3}=a^{3}b^{3}$
D. $a^{3}\cdot (-a)^{5}\cdot a^{12}=-a^{20}$
A. $a^{6}+a^{6}=2a^{12}$
B. $2^{-2}÷2^{0}×2^{3}=32$
C. $(-\frac{1}{2}ab^{2})\cdot (-2a^{2}b)^{3}=a^{3}b^{3}$
D. $a^{3}\cdot (-a)^{5}\cdot a^{12}=-a^{20}$
答案:
D
3. 已知$a = 1.6×10^{9},b = 4×10^{3}$,则$a^{2}÷2b$等于()
A. $2×10^{7}$
B. $4×10^{14}$
C. $3.2×10^{5}$
D. $3.2×10^{14}$
A. $2×10^{7}$
B. $4×10^{14}$
C. $3.2×10^{5}$
D. $3.2×10^{14}$
答案:
D
4. 下列计算正确的是()
A. $(x - 1)^{2}=x^{2}-1$
B. $a^{2}(a - 2)=a^{3}-2a^{2}+a$
C. $-2y(y + 2)=-2y^{2}+4y$
D. $n(m - 1)^{2}=m^{2}n - 2mn + n$
A. $(x - 1)^{2}=x^{2}-1$
B. $a^{2}(a - 2)=a^{3}-2a^{2}+a$
C. $-2y(y + 2)=-2y^{2}+4y$
D. $n(m - 1)^{2}=m^{2}n - 2mn + n$
答案:
D
5. 若$a,b$是正数,$a - b = 1,ab = 2$,则$a + b$等于()
A. $-3$
B. $3$
C. $\pm 3$
D. $9$
A. $-3$
B. $3$
C. $\pm 3$
D. $9$
答案:
B
6. 请你计算:$(1 - x)(1 + x),(1 - x)(1 + x + x^{2}),\cdots$,猜想$(1 - x)(1 + x + x^{2}+\cdots+x^{n})$的结果是()
A. $1 - x^{n + 1}$
B. $1 + x^{n + 1}$
C. $1 - x^{n}$
D. $1 + x^{n}$
A. $1 - x^{n + 1}$
B. $1 + x^{n + 1}$
C. $1 - x^{n}$
D. $1 + x^{n}$
答案:
A
7. 如图1-4,边长为$m + 4$的正方形纸片剪出一个边长为$m$的正方形之后,剩余部分可剪拼成一个长方形。若拼成的长方形一边长为$4$,则另一边长为____。
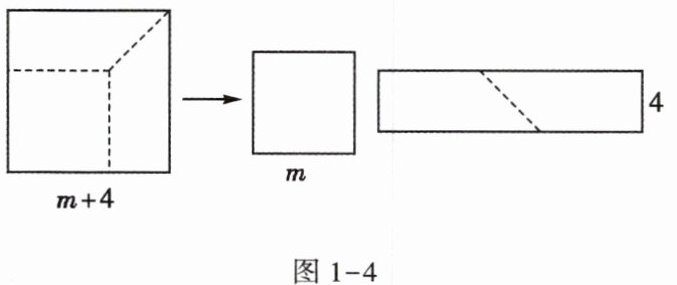

答案:
$2m + 4$
8. (1) 若$m = 2n + 1$,则$m^{2}-4mn + 4n^{2}$的值是____;
(2) 若$(x + 5)^{2}=x^{2}-mx + 25$,则$m$的值是____。
(2) 若$(x + 5)^{2}=x^{2}-mx + 25$,则$m$的值是____。
答案:
(1)1;
(2)-10
(1)1;
(2)-10
查看更多完整答案,请扫码查看


