《2025年暑假作业本大象出版社七年级数学北师大版》

13.某商场为了吸引顾客,设立了可
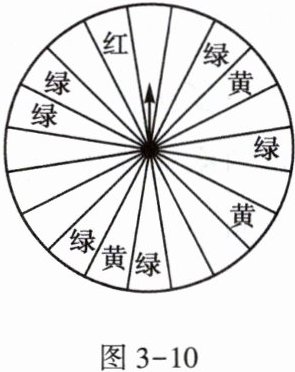
以自由转动的转盘(如图3−10,转盘被均
匀分为20份),并规定:顾客每购买200元
的商品,就能获得一次转动转盘的机会。
如果转盘停止后,指针正好对准红色、黄
色、绿色区域,那么顾客就可以分别获得
200元、100元、50元的购物券，凭购物券
可以在该商场继续购物。如果顾客不愿
意转转盘,那么可以直接获得购物券
30元。
(1)求转动一次转盘获得购物券的
概率。
(2)转转盘和直接获得购物券,你认
为哪种方式对顾客更合算？

答案： 【解析】：
(1) 转盘被均分为$20$份，其中红色、黄色、绿色区域共$1 + 3 + 6 = 10$份，根据概率公式$P(A)=\frac{m}{n}$（$n$是总情况数，$m$是事件$A$发生的情况数），转动一次转盘获得购物券的概率$P=\frac{10}{20}=\frac{1}{2}$。
(2) 计算转转盘获得购物券金额的期望：
获得$200$元购物券的概率$P_{1}=\frac{1}{20}$，获得$100$元购物券的概率$P_{2}=\frac{3}{20}$，获得$50$元购物券的概率$P_{3}=\frac{6}{20}$。
根据期望公式$E = x_{1}P_{1}+x_{2}P_{2}+\cdots + x_{n}P_{n}$，可得转转盘获得购物券金额的期望$E = 200\times\frac{1}{20}+100\times\frac{3}{20}+50\times\frac{6}{20}$
$200\times\frac{1}{20}=10$，$100\times\frac{3}{20}=15$，$50\times\frac{6}{20}=15$。
$E = 10 + 15 + 15 = 40$（元）。
因为$40\gt30$，所以转转盘对顾客更合算。
【答案】：
(1) $\frac{1}{2}$
(2) 转转盘对顾客更合算。