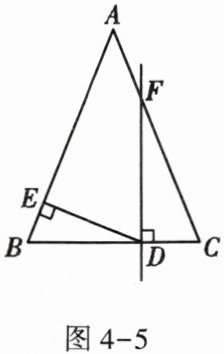
4. 如图4-5,在$\triangle ABC$中,已知$∠B = ∠C$,$FD⊥BC$,$DE⊥AB$,$∠AFD = 158^{\circ}$,求$∠EDF$的度数。

答案:
【解析】:
1. 首先求$\angle CFD$的度数:
因为$\angle AFD+\angle CFD = 180^{\circ}$(邻补角定义),已知$\angle AFD = 158^{\circ}$,所以$\angle CFD=180^{\circ}-\angle AFD = 180 - 158=22^{\circ}$。
2. 然后在$Rt\triangle FDC$中求$\angle C$的度数:
因为$FD\perp BC$,所以$\angle FDC = 90^{\circ}$。
在$\triangle FDC$中,根据三角形内角和为$180^{\circ}$,$\angle C=180^{\circ}-\angle FDC - \angle CFD$,把$\angle FDC = 90^{\circ}$,$\angle CFD = 22^{\circ}$代入可得$\angle C=180 - 90 - 22 = 68^{\circ}$。
3. 接着由$\angle B=\angle C$求$\angle B$的度数:
因为$\angle B=\angle C$,所以$\angle B = 68^{\circ}$。
4. 再在$Rt\triangle BDE$中求$\angle BDE$的度数:
因为$DE\perp AB$,所以$\angle BED = 90^{\circ}$。
在$\triangle BDE$中,根据三角形内角和为$180^{\circ}$,$\angle BDE=180^{\circ}-\angle BED-\angle B$,把$\angle BED = 90^{\circ}$,$\angle B = 68^{\circ}$代入可得$\angle BDE=180 - 90 - 68 = 22^{\circ}$。
5. 最后求$\angle EDF$的度数:
因为$\angle BDE+\angle EDF+\angle FDC = 180^{\circ}$(平角定义),$\angle FDC = 90^{\circ}$,$\angle BDE = 22^{\circ}$。
所以$\angle EDF=180^{\circ}-\angle BDE - \angle FDC=180 - 22 - 90 = 68^{\circ}$。
【答案】:$68^{\circ}$
1. 首先求$\angle CFD$的度数:
因为$\angle AFD+\angle CFD = 180^{\circ}$(邻补角定义),已知$\angle AFD = 158^{\circ}$,所以$\angle CFD=180^{\circ}-\angle AFD = 180 - 158=22^{\circ}$。
2. 然后在$Rt\triangle FDC$中求$\angle C$的度数:
因为$FD\perp BC$,所以$\angle FDC = 90^{\circ}$。
在$\triangle FDC$中,根据三角形内角和为$180^{\circ}$,$\angle C=180^{\circ}-\angle FDC - \angle CFD$,把$\angle FDC = 90^{\circ}$,$\angle CFD = 22^{\circ}$代入可得$\angle C=180 - 90 - 22 = 68^{\circ}$。
3. 接着由$\angle B=\angle C$求$\angle B$的度数:
因为$\angle B=\angle C$,所以$\angle B = 68^{\circ}$。
4. 再在$Rt\triangle BDE$中求$\angle BDE$的度数:
因为$DE\perp AB$,所以$\angle BED = 90^{\circ}$。
在$\triangle BDE$中,根据三角形内角和为$180^{\circ}$,$\angle BDE=180^{\circ}-\angle BED-\angle B$,把$\angle BED = 90^{\circ}$,$\angle B = 68^{\circ}$代入可得$\angle BDE=180 - 90 - 68 = 22^{\circ}$。
5. 最后求$\angle EDF$的度数:
因为$\angle BDE+\angle EDF+\angle FDC = 180^{\circ}$(平角定义),$\angle FDC = 90^{\circ}$,$\angle BDE = 22^{\circ}$。
所以$\angle EDF=180^{\circ}-\angle BDE - \angle FDC=180 - 22 - 90 = 68^{\circ}$。
【答案】:$68^{\circ}$
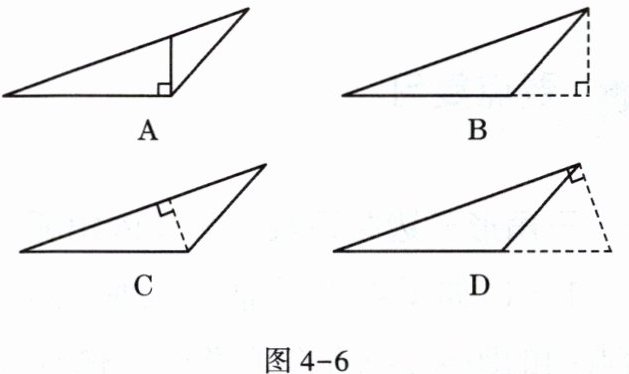
1. (1)小华在电话中问小明:“已知一个三角形三边长分别是$4,6,9$,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解。”小华根据小明的提示作出的图形正确的是图4-6中的( )
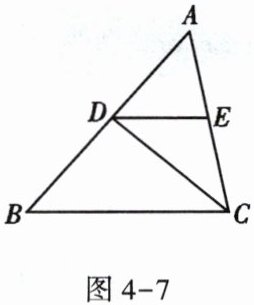
(2)如图4-7,在$\triangle ABC$中,$CD$平分$∠ACB$交$AB$于点$D$,过点$D$作$DE// BC$交$AC$于点$E$。若$∠A = 54^{\circ}$,$∠B = 48^{\circ}$,则$∠CDE$的度数为________。
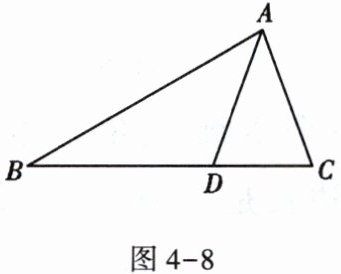
(3)如图4-8,在$\triangle ABC$中,$AD$平分$∠BAC$交$BC$于点$D$,$∠B = 30^{\circ}$,$∠ADC = 70^{\circ}$,则$∠C$的度数是________。

(2)如图4-7,在$\triangle ABC$中,$CD$平分$∠ACB$交$AB$于点$D$,过点$D$作$DE// BC$交$AC$于点$E$。若$∠A = 54^{\circ}$,$∠B = 48^{\circ}$,则$∠CDE$的度数为________。

(3)如图4-8,在$\triangle ABC$中,$AD$平分$∠BAC$交$BC$于点$D$,$∠B = 30^{\circ}$,$∠ADC = 70^{\circ}$,则$∠C$的度数是________。

答案:
$(1)$$\boldsymbol{B}$
$(2)$$\boldsymbol{39^{\circ}}$
$(3)$$\boldsymbol{70^{\circ}}$
$(2)$$\boldsymbol{39^{\circ}}$
$(3)$$\boldsymbol{70^{\circ}}$
2. (1)已知$AD$是$\triangle ABC$的中线,$\triangle ABC$的面积为$100cm^2$,则$\triangle ABD$的面积是________。
(2)如图4-9,$AD$是$\triangle ABC$的边$BC$上的中线,若$\triangle ABD$的周长比$\triangle ACD$的周长大$5$,则$AB$与$AC$的差为________。
(2)如图4-9,$AD$是$\triangle ABC$的边$BC$上的中线,若$\triangle ABD$的周长比$\triangle ACD$的周长大$5$,则$AB$与$AC$的差为________。

答案:
(1) $50cm^{2}$
(2) $5$
(1) $50cm^{2}$
(2) $5$
查看更多完整答案,请扫码查看


