3. 如图5-2,在△ABC中,点D在BC上,将点D分别以AB,AC为对称轴,画出对称点E,F,并连接AE,AF。根据图中标示的角度,则∠EAF的度数为()

A. 158°
B. 134°
C. 128°
D. 120°

A. 158°
B. 134°
C. 128°
D. 120°
答案:
B
4. 如图5-3,将△ABC折叠,使点A与BC边的中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为________。


答案:
$12$
5. 如图5-4,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD的度数为________。
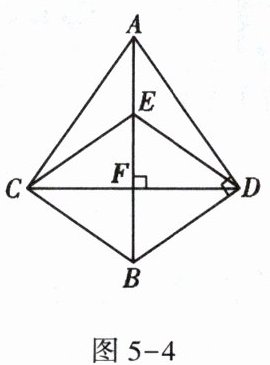

答案:
$140^{\circ}$
6. 如图5-5,∠AOB内有一点P,分别画出点P关于OA,OB的对称点P₁,P₂,连接P₁P₂交OA于点M,交OB于点N。若P₁P₂=5cm,则△PMN的周长为多少?
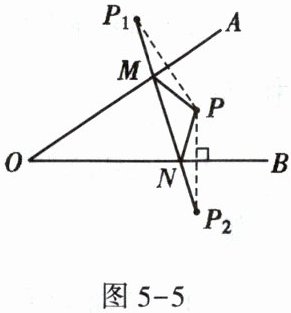

答案:
【解析】:
因为点$P$关于$OA$的对称点是$P_1$,所以$OA$是线段$PP_1$的垂直平分线,根据垂直平分线的性质可知$MP = MP_1$。
同理,点$P$关于$OB$的对称点是$P_2$,所以$OB$是线段$PP_2$的垂直平分线,那么$NP = NP_2$。
$\triangle PMN$的周长$C_{\triangle PMN}=PM + MN + NP$,将$MP = MP_1$,$NP = NP_2$代入可得:$C_{\triangle PMN}=MP_1 + MN + NP_2$。
而$MP_1 + MN + NP_2 = P_1P_2$(因为$P_1$、$M$、$N$、$P_2$在同一条直线上),已知$P_1P_2 = 5cm$。
【答案】:$5cm$
因为点$P$关于$OA$的对称点是$P_1$,所以$OA$是线段$PP_1$的垂直平分线,根据垂直平分线的性质可知$MP = MP_1$。
同理,点$P$关于$OB$的对称点是$P_2$,所以$OB$是线段$PP_2$的垂直平分线,那么$NP = NP_2$。
$\triangle PMN$的周长$C_{\triangle PMN}=PM + MN + NP$,将$MP = MP_1$,$NP = NP_2$代入可得:$C_{\triangle PMN}=MP_1 + MN + NP_2$。
而$MP_1 + MN + NP_2 = P_1P_2$(因为$P_1$、$M$、$N$、$P_2$在同一条直线上),已知$P_1P_2 = 5cm$。
【答案】:$5cm$
1. 如图5-6,在Rt△ABC中,∠ACB=90°,∠A=50°,以点B为圆心,BC的长为半径画弧,交AB于点D,连接CD,则∠BCD的度数为()

A. 80°
B. 70°
C. 65°
D. 60°

A. 80°
B. 70°
C. 65°
D. 60°
答案:
B
2. 如图5-7,BD是∠ABC的平分线,DE⊥AB于点E,S△ABC=90,AB=18,BC=12,则DE的长是()
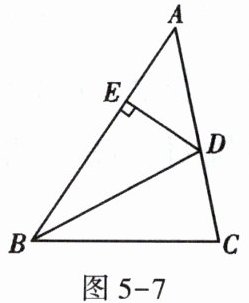
A. 3
B. 4
C. 5
D. 6

A. 3
B. 4
C. 5
D. 6
答案:
D
3. 如图5-8,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于点D,交AB于点E,下列结论错误的是()

A. BD平分∠ABC
B. △BCD的周长等于AB+BC
C. AD=BD=BC
D. D是线段AC的中点

A. BD平分∠ABC
B. △BCD的周长等于AB+BC
C. AD=BD=BC
D. D是线段AC的中点
答案:
D
查看更多完整答案,请扫码查看


