3. 下列计算正确的是()
A. $2a^{2}+a = 3a^{2}$
B. $2a - 1=\frac{1}{2}a(a≠0)$
C. $(-a^{2})^{3}÷a^{4}=-a$
D. $2a^{2}\cdot 3a^{3}=6a^{5}$
A. $2a^{2}+a = 3a^{2}$
B. $2a - 1=\frac{1}{2}a(a≠0)$
C. $(-a^{2})^{3}÷a^{4}=-a$
D. $2a^{2}\cdot 3a^{3}=6a^{5}$
答案:
D
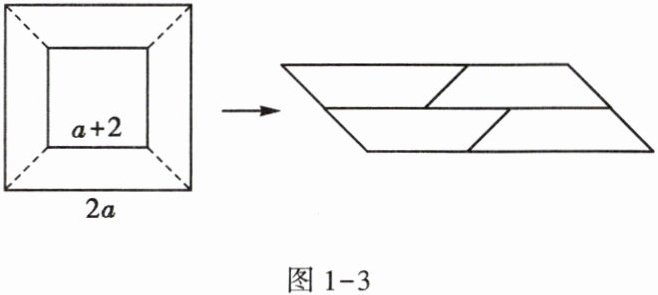
4. 如图1-3,在边长为$2a$的正方形中央剪去一个边长为$a + 2$的小正方形$(a>2)$,将剩余部分剪开无缝拼接成一个平行四边形,则该平行四边形的面积为()
A. $a^{2}+4$
B. $2a^{2}+4a$
C. $3a^{2}-4a - 4$
D. $4a^{2}-a - 2$

A. $a^{2}+4$
B. $2a^{2}+4a$
C. $3a^{2}-4a - 4$
D. $4a^{2}-a - 2$
答案:
$\boldsymbol{C}$
5. 已知$x^{2}-2 = y$,则$x(x - 3y)+y(3x - 1)-2$的值是()
A. $-2$
B. $0$
C. $2$
D. $4$
A. $-2$
B. $0$
C. $2$
D. $4$
答案:
B
6. 若$m + n = 7,mn = 12$,则$m^{2}-mn + n^{2}$的值是()
A. $11$
B. $13$
C. $37$
D. $61$
A. $11$
B. $13$
C. $37$
D. $61$
答案:
B
7. 若$2\cdot 8n\cdot 16n = 225$,则$n$的值为____。
答案:
$\frac{24}{7}$
8. 若$3^{m}=9^{n}=2$,则$3^{m + 2n}=$____。
答案:
$4$
9. 已知$(b + 3)^{2}+\vert a - 2\vert = 0$,则$a^{b}=$____。
答案:
$\frac{1}{8}$
10. 斑叶兰被列为国家二级保护植物,它的一粒种子重约$0.0000005g$。将$0.0000005$用科学记数法可表示为____。
答案:
$5\times10^{-7}$
11. 先化简,再求值:$(x - 2)(x + 2)-x(x - 1)$,其中$x = 3$。
答案:
【解析】:本题可先根据平方差公式$(a+b)(a - b)=a^2 - b^2$以及单项式乘多项式的运算法则对原式进行化简,再将$x = 3$代入化简后的式子求值。
- **步骤一:化简原式**
利用平方差公式$(a+b)(a - b)=a^2 - b^2$化简$(x - 2)(x + 2)$,可得$(x - 2)(x + 2)=x^2 - 2^2=x^2 - 4$。
根据单项式乘多项式的运算法则,用单项式$x$去乘多项式$(x - 1)$的每一项,可得$x(x - 1)=x^2 - x$。
将上述结果代入原式,可得:
$(x - 2)(x + 2)-x(x - 1)=x^2 - 4 - (x^2 - x)$
去括号得:$x^2 - 4 - x^2 + x$
合并同类项得:$(x^2 - x^2)+x - 4=x - 4$。
- **步骤二:代入求值**
将$x = 3$代入化简后的式子$x - 4$,可得:$3 - 4=-1$。
【答案】:$-1$
- **步骤一:化简原式**
利用平方差公式$(a+b)(a - b)=a^2 - b^2$化简$(x - 2)(x + 2)$,可得$(x - 2)(x + 2)=x^2 - 2^2=x^2 - 4$。
根据单项式乘多项式的运算法则,用单项式$x$去乘多项式$(x - 1)$的每一项,可得$x(x - 1)=x^2 - x$。
将上述结果代入原式,可得:
$(x - 2)(x + 2)-x(x - 1)=x^2 - 4 - (x^2 - x)$
去括号得:$x^2 - 4 - x^2 + x$
合并同类项得:$(x^2 - x^2)+x - 4=x - 4$。
- **步骤二:代入求值**
将$x = 3$代入化简后的式子$x - 4$,可得:$3 - 4=-1$。
【答案】:$-1$
12. 已知$x$满足$x^{2}-2x - 1 = 0$,求代数式$(2x - 1)^{2}-x(x + 4)+(x - 2)(x + 2)$的值。
答案:
【解析】:
本题可先化简代数式$(2x - 1)^{2}-x(x + 4)+(x - 2)(x + 2)$,再根据已知条件$x^{2}-2x - 1 = 0$求出化简后代数式的值。
- **步骤一:化简代数式$(2x - 1)^{2}-x(x + 4)+(x - 2)(x + 2)$**
根据完全平方公式$(a-b)^2=a^2-2ab+b^2$,对$(2x - 1)^{2}$进行展开:
$(2x - 1)^{2}=(2x)^{2}-2\times2x\times1 + 1^{2}=4x^{2}-4x + 1$
根据单项式乘多项式的运算法则,对$x(x + 4)$进行展开:
$x(x + 4)=x^{2}+4x$
根据平方差公式$(a+b)(a-b)=a^2-b^2$,对$(x - 2)(x + 2)$进行展开:
$(x - 2)(x + 2)=x^{2}-2^{2}=x^{2}-4$
将上述展开式代入原式可得:
$\begin{aligned}&(2x - 1)^{2}-x(x + 4)+(x - 2)(x + 2)\\=&4x^{2}-4x + 1-(x^{2}+4x)+x^{2}-4\\=&4x^{2}-4x + 1 - x^{2}-4x + x^{2}-4\\=&(4x^{2}- x^{2}+ x^{2})+(-4x - 4x)+(1 - 4)\\=&4x^{2}-8x - 3\end{aligned}$
- **步骤二:根据已知条件$x^{2}-2x - 1 = 0$求出$x^{2}-2x$的值**
由$x^{2}-2x - 1 = 0$,移项可得$x^{2}-2x = 1$。
- **步骤三:将$x^{2}-2x = 1$代入化简后的式子$4x^{2}-8x - 3$求值**
对$4x^{2}-8x - 3$进行变形可得$4(x^{2}-2x) - 3$,将$x^{2}-2x = 1$代入可得:
$4\times1 - 3 = 4 - 3 = 1$
【答案】:$1$
本题可先化简代数式$(2x - 1)^{2}-x(x + 4)+(x - 2)(x + 2)$,再根据已知条件$x^{2}-2x - 1 = 0$求出化简后代数式的值。
- **步骤一:化简代数式$(2x - 1)^{2}-x(x + 4)+(x - 2)(x + 2)$**
根据完全平方公式$(a-b)^2=a^2-2ab+b^2$,对$(2x - 1)^{2}$进行展开:
$(2x - 1)^{2}=(2x)^{2}-2\times2x\times1 + 1^{2}=4x^{2}-4x + 1$
根据单项式乘多项式的运算法则,对$x(x + 4)$进行展开:
$x(x + 4)=x^{2}+4x$
根据平方差公式$(a+b)(a-b)=a^2-b^2$,对$(x - 2)(x + 2)$进行展开:
$(x - 2)(x + 2)=x^{2}-2^{2}=x^{2}-4$
将上述展开式代入原式可得:
$\begin{aligned}&(2x - 1)^{2}-x(x + 4)+(x - 2)(x + 2)\\=&4x^{2}-4x + 1-(x^{2}+4x)+x^{2}-4\\=&4x^{2}-4x + 1 - x^{2}-4x + x^{2}-4\\=&(4x^{2}- x^{2}+ x^{2})+(-4x - 4x)+(1 - 4)\\=&4x^{2}-8x - 3\end{aligned}$
- **步骤二:根据已知条件$x^{2}-2x - 1 = 0$求出$x^{2}-2x$的值**
由$x^{2}-2x - 1 = 0$,移项可得$x^{2}-2x = 1$。
- **步骤三:将$x^{2}-2x = 1$代入化简后的式子$4x^{2}-8x - 3$求值**
对$4x^{2}-8x - 3$进行变形可得$4(x^{2}-2x) - 3$,将$x^{2}-2x = 1$代入可得:
$4\times1 - 3 = 4 - 3 = 1$
【答案】:$1$
查看更多完整答案,请扫码查看


