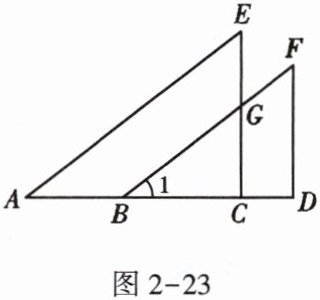
11. 如图2-23,点A,B,C,D在同一条直线上,CE与BF交于点G,$∠A=∠1$,$CE// DF$,试说明$∠E=∠F$。

答案:
【解析】:
- 因为$∠A = ∠1$,根据“同位角相等,两直线平行”,可得$AE// BF$。
- 由$AE// BF$,根据“两直线平行,内错角相等”,所以$∠E = ∠EGC$。
- 又因为$CE// DF$,根据“两直线平行,内错角相等”,则$∠EGC = ∠F$。
- 综上,通过等量代换可得$∠E = ∠F$。
【答案】:
$\because∠A = ∠1$,$\therefore AE// BF$(同位角相等,两直线平行),$\therefore∠E = ∠EGC$(两直线平行,内错角相等)。
$\because CE// DF$,$\therefore∠EGC = ∠F$(两直线平行,内错角相等),$\therefore∠E = ∠F$(等量代换)。
- 因为$∠A = ∠1$,根据“同位角相等,两直线平行”,可得$AE// BF$。
- 由$AE// BF$,根据“两直线平行,内错角相等”,所以$∠E = ∠EGC$。
- 又因为$CE// DF$,根据“两直线平行,内错角相等”,则$∠EGC = ∠F$。
- 综上,通过等量代换可得$∠E = ∠F$。
【答案】:
$\because∠A = ∠1$,$\therefore AE// BF$(同位角相等,两直线平行),$\therefore∠E = ∠EGC$(两直线平行,内错角相等)。
$\because CE// DF$,$\therefore∠EGC = ∠F$(两直线平行,内错角相等),$\therefore∠E = ∠F$(等量代换)。
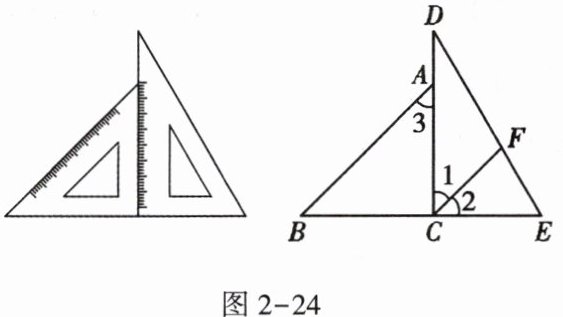
12. 将一副三角板拼成如图2-24所示的图形,过点C作CF平分$∠DCE$交DE于点F。
(1)试说明$CF// AB$;
(2)求$∠DFC$的度数。

(1)试说明$CF// AB$;
(2)求$∠DFC$的度数。
答案:
【解析】:
(1)已知三角板的角度,$\angle BAC = 45^{\circ}$,$\angle DCE = 90^{\circ}$。
因为$CF$平分$\angle DCE$,根据角平分线定义,$\angle 1=\angle 2=\frac{1}{2}\angle DCE$,所以$\angle 1 = 45^{\circ}$。
又因为$\angle BAC = 45^{\circ}$,所以$\angle 1=\angle BAC$。
根据内错角相等,两直线平行,可得$CF// AB$。
(2)在$\triangle DFC$中,已知$\angle D = 30^{\circ}$,$\angle 1 = 45^{\circ}$。
根据三角形内角和为$180^{\circ}$,则$\angle DFC=180^{\circ}-\angle D - \angle 1$。
把$\angle D = 30^{\circ}$,$\angle 1 = 45^{\circ}$代入可得:$\angle DFC=180^{\circ}-30^{\circ}-45^{\circ}=105^{\circ}$。
【答案】:
(1)$CF// AB$;(2)$105^{\circ}$
(1)已知三角板的角度,$\angle BAC = 45^{\circ}$,$\angle DCE = 90^{\circ}$。
因为$CF$平分$\angle DCE$,根据角平分线定义,$\angle 1=\angle 2=\frac{1}{2}\angle DCE$,所以$\angle 1 = 45^{\circ}$。
又因为$\angle BAC = 45^{\circ}$,所以$\angle 1=\angle BAC$。
根据内错角相等,两直线平行,可得$CF// AB$。
(2)在$\triangle DFC$中,已知$\angle D = 30^{\circ}$,$\angle 1 = 45^{\circ}$。
根据三角形内角和为$180^{\circ}$,则$\angle DFC=180^{\circ}-\angle D - \angle 1$。
把$\angle D = 30^{\circ}$,$\angle 1 = 45^{\circ}$代入可得:$\angle DFC=180^{\circ}-30^{\circ}-45^{\circ}=105^{\circ}$。
【答案】:
(1)$CF// AB$;(2)$105^{\circ}$
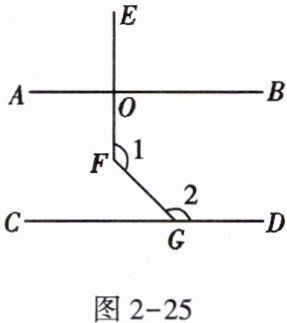
13. 如图2-25,$AB// CD$,$EF⊥AB$于点O,$∠2=135^{\circ}$,求$∠1$的度数。
下面提供三个思路:①过点F作$FH// AB$;②延长EF交CD于点I;③延长GF交AB于点K。请你利用三个思路中的任意一个,求$∠1$的度数。
下面提供三个思路:①过点F作$FH// AB$;②延长EF交CD于点I;③延长GF交AB于点K。请你利用三个思路中的任意一个,求$∠1$的度数。

答案:
【解析】:
### 方法一:过点$F$作$FH// AB$
因为$AB// CD$,$FH// AB$,根据平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行,所以$FH// CD$。
因为$FH// CD$,所以$\angle2+\angle HFG = 180^{\circ}$(两直线平行,同旁内角互补)。
已知$\angle2 = 135^{\circ}$,则$\angle HFG=180^{\circ}-\angle2 = 180^{\circ}-135^{\circ}=45^{\circ}$。
因为$EF\perp AB$,$FH// AB$,所以$\angle EFH=\angle EOB = 90^{\circ}$(两直线平行,同位角相等)。
那么$\angle1 = 180^{\circ}-\angle EFH-\angle HFG=180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}$。
### 方法二:延长$EF$交$CD$于点$I$
因为$AB// CD$,$EF\perp AB$,所以$\angle EID=\angle EOB = 90^{\circ}$(两直线平行,同位角相等)。
因为$\angle2$与$\angle FGD$是邻补角,所以$\angle FGD = 180^{\circ}-\angle2=180^{\circ}-135^{\circ}=45^{\circ}$。
在$\triangle FIG$中,根据三角形外角性质:三角形的一个外角等于与它不相邻的两个内角之和,$\angle EID=\angle1+\angle FGD$。
所以$\angle1=\angle EID - \angle FGD=90^{\circ}-45^{\circ}=45^{\circ}$。
### 方法三:延长$GF$交$AB$于点$K$
因为$AB// CD$,所以$\angle2+\angle AKG = 180^{\circ}$(两直线平行,同旁内角互补)。
已知$\angle2 = 135^{\circ}$,则$\angle AKG=180^{\circ}-\angle2 = 180^{\circ}-135^{\circ}=45^{\circ}$。
因为$EF\perp AB$,在$Rt\triangle FOK$中,$\angle1 = 90^{\circ}-\angle AKG$(直角三角形两锐角互余)。
所以$\angle1=90^{\circ}-45^{\circ}=45^{\circ}$。
【答案】:$45^{\circ}$
### 方法一:过点$F$作$FH// AB$
因为$AB// CD$,$FH// AB$,根据平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行,所以$FH// CD$。
因为$FH// CD$,所以$\angle2+\angle HFG = 180^{\circ}$(两直线平行,同旁内角互补)。
已知$\angle2 = 135^{\circ}$,则$\angle HFG=180^{\circ}-\angle2 = 180^{\circ}-135^{\circ}=45^{\circ}$。
因为$EF\perp AB$,$FH// AB$,所以$\angle EFH=\angle EOB = 90^{\circ}$(两直线平行,同位角相等)。
那么$\angle1 = 180^{\circ}-\angle EFH-\angle HFG=180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}$。
### 方法二:延长$EF$交$CD$于点$I$
因为$AB// CD$,$EF\perp AB$,所以$\angle EID=\angle EOB = 90^{\circ}$(两直线平行,同位角相等)。
因为$\angle2$与$\angle FGD$是邻补角,所以$\angle FGD = 180^{\circ}-\angle2=180^{\circ}-135^{\circ}=45^{\circ}$。
在$\triangle FIG$中,根据三角形外角性质:三角形的一个外角等于与它不相邻的两个内角之和,$\angle EID=\angle1+\angle FGD$。
所以$\angle1=\angle EID - \angle FGD=90^{\circ}-45^{\circ}=45^{\circ}$。
### 方法三:延长$GF$交$AB$于点$K$
因为$AB// CD$,所以$\angle2+\angle AKG = 180^{\circ}$(两直线平行,同旁内角互补)。
已知$\angle2 = 135^{\circ}$,则$\angle AKG=180^{\circ}-\angle2 = 180^{\circ}-135^{\circ}=45^{\circ}$。
因为$EF\perp AB$,在$Rt\triangle FOK$中,$\angle1 = 90^{\circ}-\angle AKG$(直角三角形两锐角互余)。
所以$\angle1=90^{\circ}-45^{\circ}=45^{\circ}$。
【答案】:$45^{\circ}$
查看更多完整答案,请扫码查看


