4. (1) 计算:$(2m + n)(2m - n)+(m + n)^{2}-2(2m^{2}-mn)$;
(2) 若$a + b = 17,ab = 60$,求$a^{2}+b^{2}$和$(a - b)^{2}$的值。
(2) 若$a + b = 17,ab = 60$,求$a^{2}+b^{2}$和$(a - b)^{2}$的值。
答案:
【解析】:
(1) 首先,根据平方差公式$(a+b)(a - b)=a^{2}-b^{2}$,可得$(2m + n)(2m - n)=(2m)^{2}-n^{2}=4m^{2}-n^{2}$;
根据完全平方公式$(a + b)^{2}=a^{2}+2ab + b^{2}$,可得$(m + n)^{2}=m^{2}+2mn + n^{2}$;
然后对原式进行化简:
$\begin{aligned}&(2m + n)(2m - n)+(m + n)^{2}-2(2m^{2}-mn)\\=&4m^{2}-n^{2}+m^{2}+2mn + n^{2}-4m^{2}+2mn\\=&(4m^{2}+m^{2}-4m^{2})+( - n^{2}+n^{2})+(2mn + 2mn)\\=&m^{2}+4mn\end{aligned}$
(2) 根据完全平方公式$(a + b)^{2}=a^{2}+2ab + b^{2}$,可得$a^{2}+b^{2}=(a + b)^{2}-2ab$。
已知$a + b = 17$,$ab = 60$,将其代入上式可得:
$a^{2}+b^{2}=17^{2}-2\times60=289 - 120 = 169$。
根据完全平方公式$(a - b)^{2}=a^{2}-2ab + b^{2}=a^{2}+2ab + b^{2}-4ab=(a + b)^{2}-4ab$。
把$a + b = 17$,$ab = 60$代入可得:
$(a - b)^{2}=17^{2}-4\times60=289 - 240 = 49$。
【答案】:
(1)$m^{2}+4mn$;
(2)$a^{2}+b^{2}=169$,$(a - b)^{2}=49$
(1) 首先,根据平方差公式$(a+b)(a - b)=a^{2}-b^{2}$,可得$(2m + n)(2m - n)=(2m)^{2}-n^{2}=4m^{2}-n^{2}$;
根据完全平方公式$(a + b)^{2}=a^{2}+2ab + b^{2}$,可得$(m + n)^{2}=m^{2}+2mn + n^{2}$;
然后对原式进行化简:
$\begin{aligned}&(2m + n)(2m - n)+(m + n)^{2}-2(2m^{2}-mn)\\=&4m^{2}-n^{2}+m^{2}+2mn + n^{2}-4m^{2}+2mn\\=&(4m^{2}+m^{2}-4m^{2})+( - n^{2}+n^{2})+(2mn + 2mn)\\=&m^{2}+4mn\end{aligned}$
(2) 根据完全平方公式$(a + b)^{2}=a^{2}+2ab + b^{2}$,可得$a^{2}+b^{2}=(a + b)^{2}-2ab$。
已知$a + b = 17$,$ab = 60$,将其代入上式可得:
$a^{2}+b^{2}=17^{2}-2\times60=289 - 120 = 169$。
根据完全平方公式$(a - b)^{2}=a^{2}-2ab + b^{2}=a^{2}+2ab + b^{2}-4ab=(a + b)^{2}-4ab$。
把$a + b = 17$,$ab = 60$代入可得:
$(a - b)^{2}=17^{2}-4\times60=289 - 240 = 49$。
【答案】:
(1)$m^{2}+4mn$;
(2)$a^{2}+b^{2}=169$,$(a - b)^{2}=49$
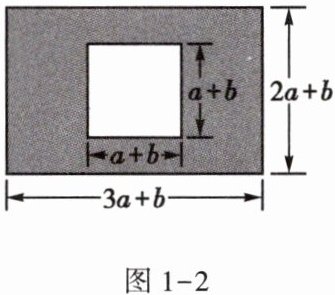
5. 某小区中有一块长为$(3a + b)m$、宽为$(2a + b)m$的长方形空地,物业部门计划将其进行绿化(如图1-2阴影部分),但中间部分将修建一个仿古小景点(图中间的正方形),则绿化的面积是多少平方米?请求出当$a = 3,b = 2$时的绿化面积。

答案:
【解析】:
首先,根据长方形面积公式$S = 长\times宽$,可得长方形空地的面积$S_{长}=(3a + b)(2a + b)$,根据多项式乘法法则展开:
$\begin{aligned}(3a + b)(2a + b)&=3a\times(2a + b)+b\times(2a + b)\\&=6a^{2}+3ab + 2ab + b^{2}\\&=6a^{2}+5ab + b^{2}\end{aligned}$
然后,根据正方形面积公式$S = 边长\times边长$,可得正方形小景点的面积$S_{正}=(a + b)(a + b)$,根据完全平方公式展开:
$\begin{aligned}(a + b)(a + b)&=a^{2}+2ab + b^{2}\end{aligned}$
最后,绿化面积$S = S_{长}-S_{正}$,即:
$\begin{aligned}S&=(6a^{2}+5ab + b^{2})-(a^{2}+2ab + b^{2})\\&=6a^{2}+5ab + b^{2}-a^{2}-2ab - b^{2}\\&=(6a^{2}-a^{2})+(5ab - 2ab)+(b^{2}-b^{2})\\&=5a^{2}+3ab\end{aligned}$
当$a = 3$,$b = 2$时,代入$S = 5a^{2}+3ab$可得:
$\begin{aligned}S&=5\times3^{2}+3\times3\times2\\&=5\times9+18\\&=45 + 18\\&=63\end{aligned}$
【答案】:绿化面积是$(5a^{2}+3ab)$平方米,当$a = 3$,$b = 2$时绿化面积是$63$平方米。
首先,根据长方形面积公式$S = 长\times宽$,可得长方形空地的面积$S_{长}=(3a + b)(2a + b)$,根据多项式乘法法则展开:
$\begin{aligned}(3a + b)(2a + b)&=3a\times(2a + b)+b\times(2a + b)\\&=6a^{2}+3ab + 2ab + b^{2}\\&=6a^{2}+5ab + b^{2}\end{aligned}$
然后,根据正方形面积公式$S = 边长\times边长$,可得正方形小景点的面积$S_{正}=(a + b)(a + b)$,根据完全平方公式展开:
$\begin{aligned}(a + b)(a + b)&=a^{2}+2ab + b^{2}\end{aligned}$
最后,绿化面积$S = S_{长}-S_{正}$,即:
$\begin{aligned}S&=(6a^{2}+5ab + b^{2})-(a^{2}+2ab + b^{2})\\&=6a^{2}+5ab + b^{2}-a^{2}-2ab - b^{2}\\&=(6a^{2}-a^{2})+(5ab - 2ab)+(b^{2}-b^{2})\\&=5a^{2}+3ab\end{aligned}$
当$a = 3$,$b = 2$时,代入$S = 5a^{2}+3ab$可得:
$\begin{aligned}S&=5\times3^{2}+3\times3\times2\\&=5\times9+18\\&=45 + 18\\&=63\end{aligned}$
【答案】:绿化面积是$(5a^{2}+3ab)$平方米,当$a = 3$,$b = 2$时绿化面积是$63$平方米。
1. 小明总结以下结论:①$a(b + c)=ab + ac$;②$a(b - c)=ab - ac$;③$(b - c)÷a = b÷a - c÷a(a≠0)$;④$a÷(b + c)=a÷b + a÷c(a≠0)$。其中一定成立的结论的个数是()
A. 1
B. 2
C. 3
D. 4
A. 1
B. 2
C. 3
D. 4
答案:
C
2. (1) $(-2a)^{3}b^{4}÷12a^{3}b^{2}=$____;
(2) $(36x^{4}y^{3}-24x^{3}y^{2}+3x^{2}y^{2})÷(-6x^{2}y)=$____。
(2) $(36x^{4}y^{3}-24x^{3}y^{2}+3x^{2}y^{2})÷(-6x^{2}y)=$____。
答案:
(1)$-\frac{2}{3}b^{2}$;
(2)$-6x^{2}y^{2}+4xy-\frac{1}{2}y$
(1)$-\frac{2}{3}b^{2}$;
(2)$-6x^{2}y^{2}+4xy-\frac{1}{2}y$
3. 先化简,再求值:$(a + b)(a - b)+(4ab^{3}-8a^{2}b^{2})÷4ab$,其中$a = 2,b = 1$。
答案:
【解析】:
本题可先根据平方差公式和多项式除以单项式的运算法则对原式进行化简,再将$a$、$b$的值代入化简后的式子求值。
- **步骤一:化简原式**
**利用平方差公式化简$(a + b)(a - b)$:**
平方差公式为$(m+n)(m-n)=m^2-n^2$,在$(a + b)(a - b)$中,$m=a$,$n=b$,所以$(a + b)(a - b)=a^2 - b^2$。
**化简$(4ab^{3}-8a^{2}b^{2})\div4ab$:**
根据多项式除以单项式的运算法则,将多项式的每一项分别除以单项式,再将所得的商相加,可得:
$(4ab^{3}-8a^{2}b^{2})\div4ab=4ab^{3}\div4ab - 8a^{2}b^{2}\div4ab=b^2 - 2ab$。
**将上述化简结果代入原式并合并同类项:**
$(a + b)(a - b)+(4ab^{3}-8a^{2}b^{2})\div4ab=a^2 - b^2 + b^2 - 2ab=a^2 - 2ab$。
- **步骤二:代入求值**
将$a = 2$,$b = 1$代入化简后的式子$a^2 - 2ab$,可得:
$2^2 - 2\times2\times1=4 - 4 = 0$。
【答案】:$0$
本题可先根据平方差公式和多项式除以单项式的运算法则对原式进行化简,再将$a$、$b$的值代入化简后的式子求值。
- **步骤一:化简原式**
**利用平方差公式化简$(a + b)(a - b)$:**
平方差公式为$(m+n)(m-n)=m^2-n^2$,在$(a + b)(a - b)$中,$m=a$,$n=b$,所以$(a + b)(a - b)=a^2 - b^2$。
**化简$(4ab^{3}-8a^{2}b^{2})\div4ab$:**
根据多项式除以单项式的运算法则,将多项式的每一项分别除以单项式,再将所得的商相加,可得:
$(4ab^{3}-8a^{2}b^{2})\div4ab=4ab^{3}\div4ab - 8a^{2}b^{2}\div4ab=b^2 - 2ab$。
**将上述化简结果代入原式并合并同类项:**
$(a + b)(a - b)+(4ab^{3}-8a^{2}b^{2})\div4ab=a^2 - b^2 + b^2 - 2ab=a^2 - 2ab$。
- **步骤二:代入求值**
将$a = 2$,$b = 1$代入化简后的式子$a^2 - 2ab$,可得:
$2^2 - 2\times2\times1=4 - 4 = 0$。
【答案】:$0$
1. 下列计算结果正确的是()
A. $3x - 2x = 1$
B. $x^{3}÷x^{2}=x$
C. $x^{3}\cdot x^{2}=x^{6}$
D. $x^{2}+y^{2}=(x + y)^{2}$
A. $3x - 2x = 1$
B. $x^{3}÷x^{2}=x$
C. $x^{3}\cdot x^{2}=x^{6}$
D. $x^{2}+y^{2}=(x + y)^{2}$
答案:
B
2. 下列计算正确的是()
A. $(-a^{2})^{3}=-a^{5}$
B. $a^{3}\cdot a^{5}=a^{15}$
C. $(-a^{2}b^{3})^{2}=a^{4}b^{6}$
D. $3b^{2}-2b^{2}=1$
A. $(-a^{2})^{3}=-a^{5}$
B. $a^{3}\cdot a^{5}=a^{15}$
C. $(-a^{2}b^{3})^{2}=a^{4}b^{6}$
D. $3b^{2}-2b^{2}=1$
答案:
C
查看更多完整答案,请扫码查看


